Correlated Quantum Matter and Materials
Welcome to CQM2 Group!
 Strong interactions among atomic particles can lead to materials, such as some high-temperature superconductors, with unusual electronic and magnetic properties. Our research group at ITP and BeihangU is focusing on emergent many-body physics and ultra quantum states of matter due to the intriguing interplay between correlation and topology. We aim to develop quantum many-body simulation techniques, e.g., tensor networks, renormalization group, and deep learning techniques, that provide reliable and accurate numerical access to thermal and dynamical properties of correlated systems. With state-of-the-art methods, we explore novel states of matter and reveal underlying manybody theory, in correlated materials that could possibily lead to intriguing applications in future quantum technology.
Strong interactions among atomic particles can lead to materials, such as some high-temperature superconductors, with unusual electronic and magnetic properties. Our research group at ITP and BeihangU is focusing on emergent many-body physics and ultra quantum states of matter due to the intriguing interplay between correlation and topology. We aim to develop quantum many-body simulation techniques, e.g., tensor networks, renormalization group, and deep learning techniques, that provide reliable and accurate numerical access to thermal and dynamical properties of correlated systems. With state-of-the-art methods, we explore novel states of matter and reveal underlying manybody theory, in correlated materials that could possibily lead to intriguing applications in future quantum technology.
Research Interest:
- Quantum Many-body Theory and Computations
- Ground-State and Thermal Tensor Networks
- Frustrated Magnetism and Quantum Spin Liquids
- Correlated Electrons and Superconductivity
- Magnetocaloric Quantum Materials
Projects:
- Non-abelian symmetry and tensor networks, NSFC Junior Project: 11504014, 2016.01-2018.12
- Quantum Manybody Computation Methods and Applications, NSFC Key Project: 11834014, 2019.01-2022.12
- Thermal Tensor Networks for Frustrated Quantum Magnets, NSFC General Project: 11974036, 2020.01-2023.12
News
-
Our recent work “Significant inverse magnetocaloric effect induced by quantum criticality” is published in Phys. Rev. Research 3, 033094, 27 July 2021.
-
Our recent work “Kondo Holes in the Two-Dimensional Itinerant Ising Ferromagnet Fe3GeTe2” is published in Nano Letters 14, 6117, 19 July 2021.
-
Our recent work “Identification of magnetic interactions and high-field quantum spin liquid in α-RuCl3” is published in Nature Communications 12, 4007, 29 June 2021. BIG Congradualtions to Han Li, Yuan Gao, and Dai-Wei Qu! This is our third Nature Communications paper on frustrated quantum magnetism in the past two years. Please check the promotion of our work in the BUAA and ITP news here.
-
Our recent work “Symmetry-Protected Topological Edge Modes and Emergent Partial Time-Reversal Symmetry Breaking in Open Quantum Many-Body Systems” is published in Phys. Rev. Lett. 126, 237201, 9 June 2021. BIG Congradulations to Qiao-Yi! This work was done in collaboration with Prof. Zi Cai’s group in SJTU.
-
祝贺高源同学获得第十六届全国磁学理论会议 (https://mt2020.yzu.edu.cn/ 扬州) 优秀墙报奖.
-
Our recent work “Quantum many-body simulations of the two-dimensional Fermi-Hubbard model in ultracold optical lattices” is published in Phys. Rev. B 103, L041107, 19 Jan 2021.
Featured

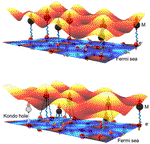
Kondo Holes in the Two-Dimensional Itinerant Ising Ferromagnet Fe3GeTe2
Heavy Fermion (HF) states emerge in correlated quantum materials due to the intriguing interplay between localized magnetic moments and itinerant electrons but rarely appear in 3d-electron systems due to high itinerancy of d-electrons. An itinerant Kondo–Ising model is established to reproduce the experimental results, explains the microscopic origin of the d-electron HF states in Fe3GeTe2, and inspires future studies of the enriched quantum many-body effects with Kondo holes.

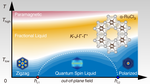
Identification of magnetic interactions and high-field quantum spin liquid in α-RuCl3
The nature of spin interactions and the field-induced quantum spin liquid phase in a Kitaev material α-RuCl3 have been debated. Here, using a combination of many-body techniques, the authors derive an effective spin model that explains the majority of experimental findings and predicts a new quantum spin liquid phase in strong out-of-plane magnetic field.

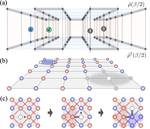
Symmetry-Protected Topological Edge Modes and Emergent Partial Time-Reversal Symmetry Breaking in Open Quantum Many-Body Systems
Symmetry-protected topological edge modes are one of the most remarkable phenomena in topological physics. Here, we formulate and quantitatively examine the effect of a quantum bath on these topological edge modes. Using the density matrix renormalization group method, we show that the time-reversal symmetry (TRS) plays a special role for an open quantum system, where an emergent partial TRS breaking will result in a TRS-protected topological mode diffusing from the system edge into the bath, thus make it useless for quantum computation.

Quantum Many-Body Simulations of the Two-Dimensional Fermi-Hubbard Model in Ultracold Optical Lattices
Understanding quantum many-body states of correlated electrons is one main theme in modern condensed-matter physics. We demonstrate the exponential tensor renormalization group (XTRG) algorithm [Chen et al., Phys. Rev. X 8, 031082 (2018)], complemented by independent determinant quantum Monte Carlo, offers a powerful combination of tools for studying the Fermi-Hubbard model. XTRG provides full and accurate access to the density matrix and thus various spin and charge correlations, down to an unprecedented low temperature of a few percent of the tunneling energy. We observe excellent agreement with ultracold fermion quantum simulations at both half filling and finite doping.

Evidence of the Berezinskii-Kosterlitz-Thouless phase in a frustrated magnet
The Berezinskii-Kosterlitz-Thouless (BKT) phase transition has long been sought yet undiscovered directly in magnetic materials. Here, the authors identify two phase transitions with BKT fluctuations detected by NMR and critical scaling behavior in magnetic susceptibility expected for the BKT transition in a frustrated magnet TmMgGaO4.

Universal thermodynamics in the Kitaev fractional liquid
With recently developed exponential tensor-network approach, the authors perform accurate finite-temperature simulations of the extended Kitaev model with additional interactions common in Kitaev materials. At intermediate temperature, they find an emergent Curie law of magnetic susceptibility and a stripy spin-structure factor characterizing the robust Kitaev fractional liquid.

Kosterlitz-Thouless melting of magnetic order in the triangular quantum Ising material TmMgGaO$_4$
TmMgGaO4 is one of a number of recently-synthesized quantum magnets that are proposed to realize important theoretical models. Here the authors demonstrate the agreement between detailed experimental measurements and state-of-the-art predictions based on the 2D transverse field triangular lattice Ising model.

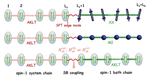
Two-Temperature Scales in the Triangular-Lattice Heisenberg Antiferromagnet
The anomalous thermodynamic properties of the paradigmatic frustrated spin-1/2 triangular-lattice Heisenberg antiferromagnet (TLH) has remained an open topic of research over decades, both experimentally and theoretically. Here, we further the theoretical understanding based on the recently developed, powerful exponential tensor renormalization group method on cylinders and stripes in a quasi-one-dimensional (1D) setup, as well as a tensor product operator approach directly in 2D. The observed thermal properties of the TLH are in excellent agreement with two recent experimental measurements on the virtually ideal TLH material Ba8CoNb6O24.

Exponential Thermal Tensor Network Approach for Quantum Lattice Models
We speed up thermal simulations of quantum many-body systems in both one- (1D) and two-dimensional (2D) models in an exponential way by iteratively projecting the thermal density matrix $\rho=e^{-\beta H}$ onto itself. We refer to this scheme of doubling $\beta$ in each step of the imaginary time evolution as the exponential tensor renormalization group (XTRG). This approach is in stark contrast to conventional Trotter-Suzuki-type methods which evolve $\rho$ on a linear quasicontinuous grid in inverse temperature $\beta\equiv1/T$.