第一章 晶体结构
Crystal Structure
1. 晶体结构的基本概念

-
布拉维格子(Bravais lattice):晶体的美妙算法
-
在漂亮的晶体之下,是原子有序排列的微观结构。
非凡一念:晶体不断细分,由同样晶面角度、与整体具有相似形状的元胞 -
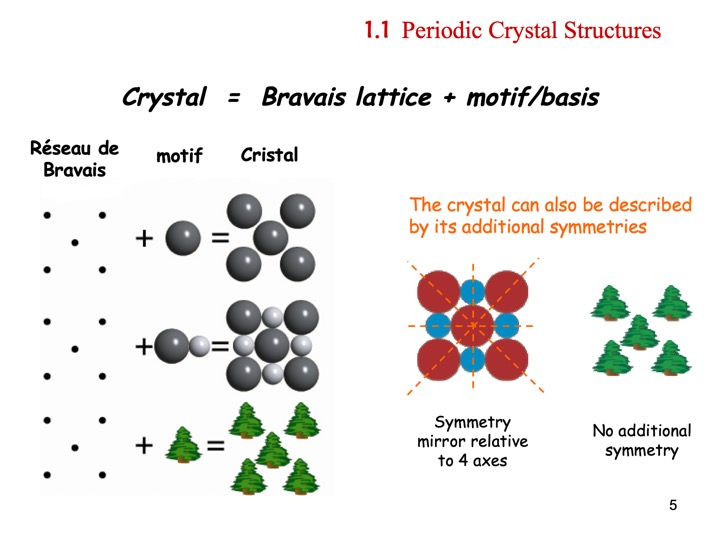
晶体结构=布拉维格子+基元
类似于“程序=算法+语言”:自然界在创造如单晶矿石等晶体物质时候,基元是具体的物质内容,而由抽象的点构成的布拉维格子则是生成晶体的数学“算法”。按照指定的算法,将基元周期排列展开,就形成万千固态材料。
-
布拉维格子有若干彼此等价的定义:
(a) 直观定义:布拉维格子是格点的无限周期排列,其中每一个点都等价。即从任何一个格点看出去,晶格都是一模一样的,周边的环境都严格相同。
(b) 数学定义:布拉维格子中的任意格点都可以表示为$R = \sum_i n_i \textbf{a}_i + r_0$,且公式不产生不属于格子中的点。式中${ a_i }$为$d$个($d$为空间维度)线性无关的向量,称为初基矢量(primitive vector),$n_i$为整数。$r_0$为某常数,当原点取在任一格点上时$r_0=0$。
(c) 抽象定义:在加法下封闭的不共面的一组离散矢量集合构成布拉维格子。
-
非布拉维格子的描述:
非布拉维格子中的任意格点都可以表示为$R = \sum_i n_i \textbf{a}_i + \sum_j r_j$,表示先按照初基矢量集合{$\textbf{a}_i$}访问最近的布拉维格点,然后再按照{$r_j$}依次访问基元中$n$个不同的点($j$从0跑到$n-1$)。
-
-
常见二维格子
-
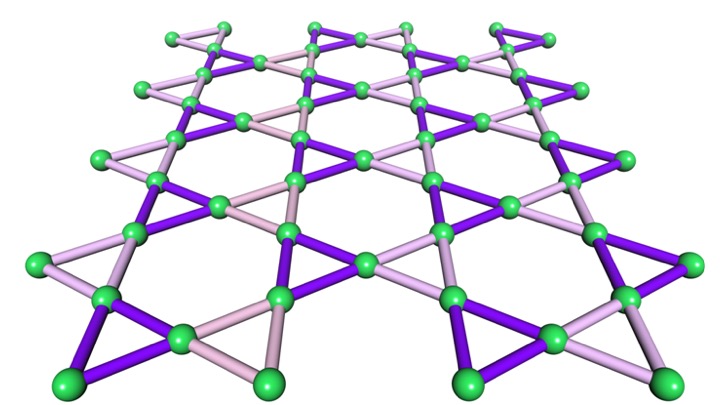
并非所有周期排列的格子都是布拉维格子。如下图所示,正方和三角为布拉维格子,但六角格子为非布拉维格子。
-
可以将六角格子中的两个点(下图中红色和蓝色)看做一个基元,按照三角布拉维格子将其“生成”出来。因此,六角格子可以视为两套三角布拉维格子嵌套而成,有时人们称这类非布拉维格子为复式格子。
-
单元素晶体将原子视为基元,其微观周期结构可能为布拉维格子或复式格子;多元素晶体总需要将多个原子视为基元,按照布拉维格子周期排列生成。

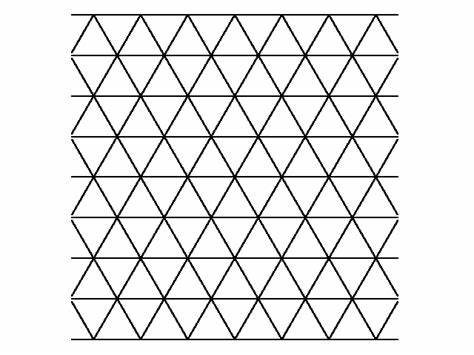
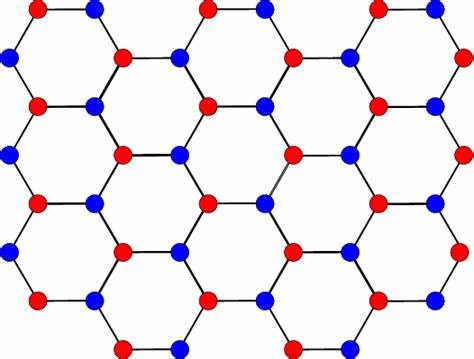
正方格子 三角格子 六角格子
-
-
常见三维格子
-
常见三维格子有简单立方,面心立方,体心立方,六角密堆积等。
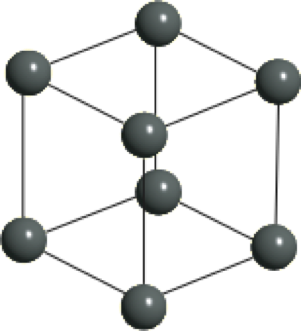
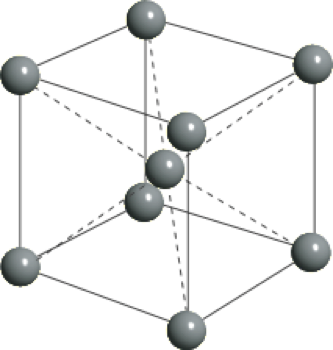
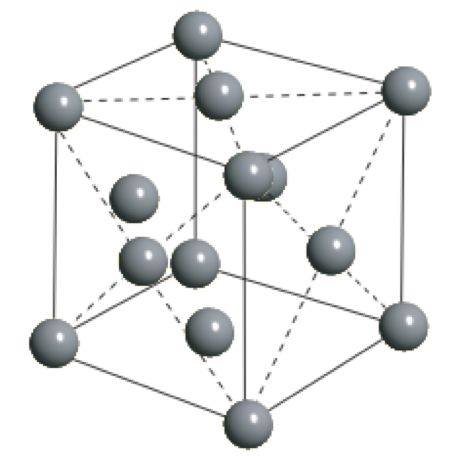
简单立方(Simple Cubic, SC) 体心立方(Body-Centered Cubic, BCC) 面心立方(Face-Centered Cubic, FCC) 上述三种三维晶格,简单立方,体心立方,和面心立方,均为布拉维格子,每个基元仅仅包含一个原子。但有时为了方便讨论,会将体心立方与面心立方中的若干原子组合视为基元,按照简单立方布拉维格子展开生成,更好地体现了体心和面心立方的对称性,使用更为方便习惯(conventional)。
-
密堆积结构是一类非常特殊的晶体结构,常见的有六角密堆积和面心立方(没错,就是上面提到的FCC!)。

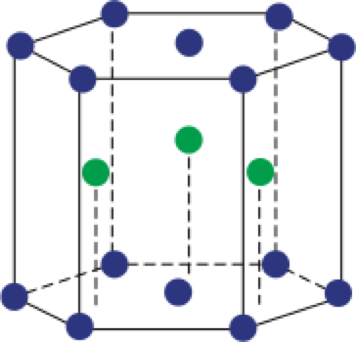
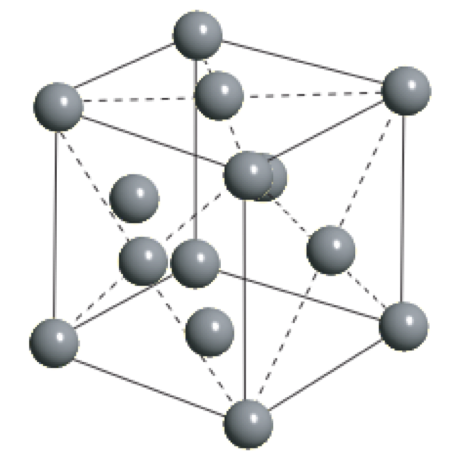
密堆积 六方密堆积(Hexagonal Compact Packing, HCP) 面心立方(Face-Centered Cubic, FCC) 从密堆积方式理解两种结构
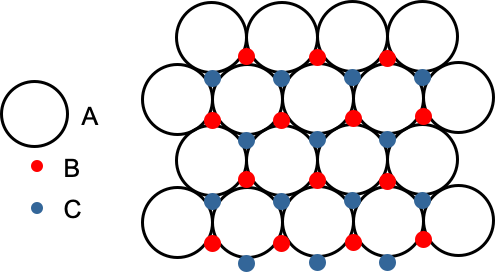
密堆积的A、B、C三种占位点 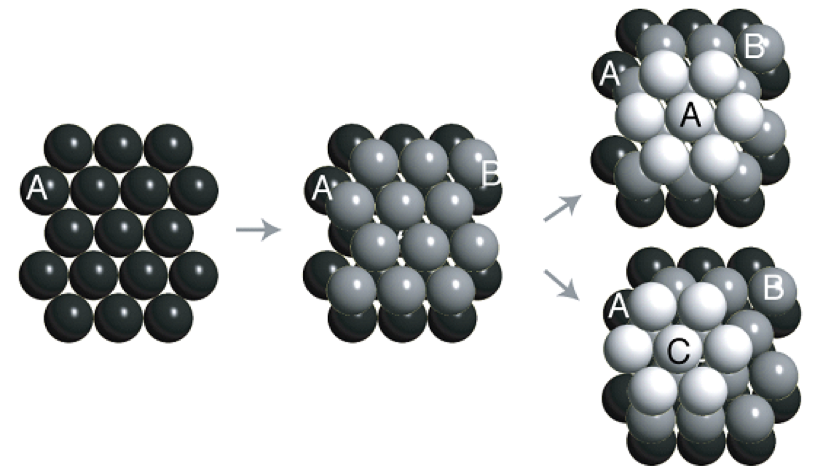
两种不同的密堆积分别形成六方密堆积和面心立方(还有无数种密堆积方式)
-
2. 常见晶体结构
下面列举几种常见的晶体材料结构。
-
金刚石结构

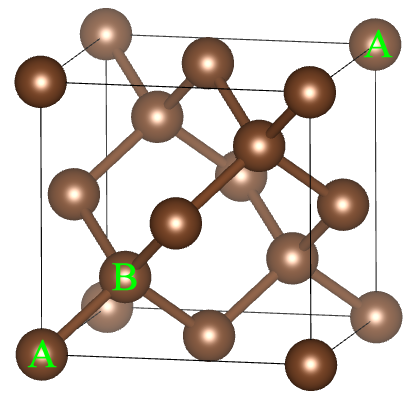
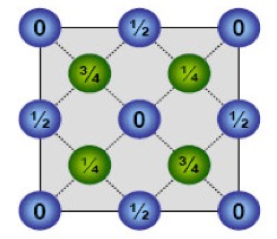
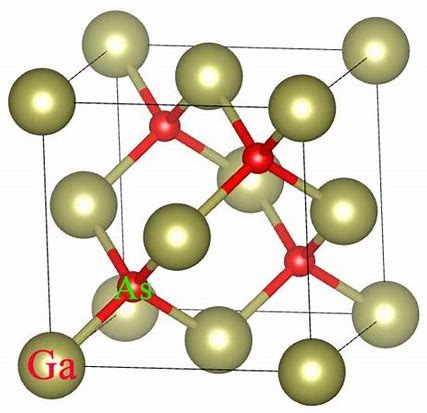
金刚石 $a=3.57 \overset{\circ}{\rm{A}}$ 俯视图 类似结构:闪锌矿 -
金刚石结构由单质碳(C)组成,具有非常高的硬度。类似的单质结构还有硅(Si,$a=5.43 \overset{\circ}{\rm{A}}$),锗(Ge,$a=5.66 \overset{\circ}{\rm{A}}$)等晶体。
-
典型的闪锌矿结构晶体包括:碳化硅(SiC,$a=4.35 \overset{\circ}{\rm{A}}$),砷化镓(GaAs,$a=5.65 \overset{\circ}{\rm{A}}$)等晶体。
-
将每个碳原子视为抽象点,金刚石结构并非布拉维格子
-
选取2个碳原子组成基元($r_0=(0,0,0)$和$r_1=(1/4,1/4,1/4)$),对应布拉维格子为面心立方
-
选取8个碳原子为基元(如何选取 {$r_j$}?),对应布拉维格子为简单立方。
-
-
NaCl晶体结构

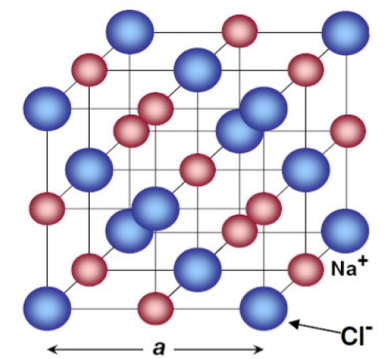
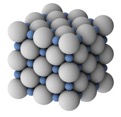
食盐晶体 $a=5.63\overset{\circ}{\rm{A}}$ 硬球模型 - 具有和食盐类似晶体结构的有:氧化镁(MgO,$a=4.20\overset{\circ}{\rm{A}}$),氯化钾(KCl,$a=6.29\overset{\circ}{\rm{A}}$)等晶体。
- 氯化钠晶体由Na和Cl两种元素组成,取二者各1组成基元,则布拉维格子为面心立方。
-
CsCl晶体结构

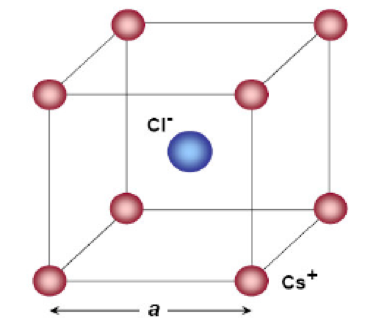

氯化铯晶体 $a=4.11 \overset{\circ}{\rm{A}}$ 硬球模型 -
粉末状的样品由微小的单晶组成。
-
取Cs和Cl两种元素个1个原子组成基元,则布拉维格子为简单立方(注意:CsCl晶体不是体心立方结构)。
-
-
二维晶体材料——石墨烯(单层石墨)
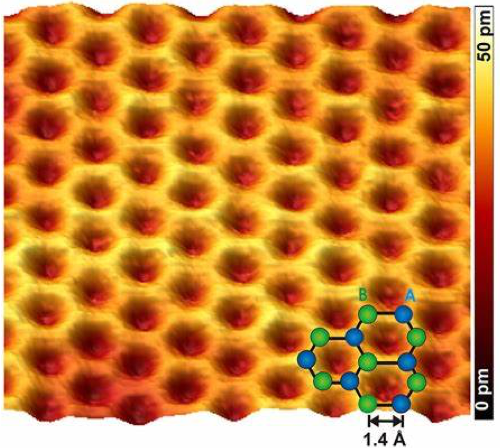
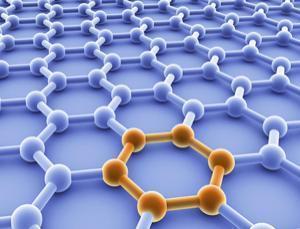
石墨烯的扫描隧道显微镜照片 单层石墨烯结构示意图 -
英国物理学家安德烈·盖姆和康斯坦丁·诺沃肖洛夫,用微机械剥离法成功从石墨中分离出石墨烯。共同获得2010年诺贝尔物理学奖。
-
石墨烯具有高强度,高电导等优异的材料性能。
-
-
双层魔转角石墨烯
 |
 |
|---|---|
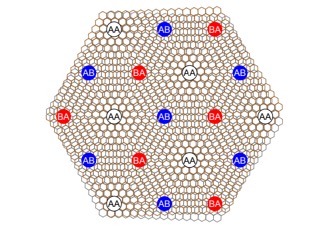
| 莫里超晶格 | AA,AB,BA 标记不同区域 |
- 由于双层魔转角石墨烯的独特电子关联性质和非常规超导电性,引起了凝聚态物理学界的广泛关注,可以阅读Physics Today 的科普文章。
3. 原胞、晶胞和填充率
-
原胞(primitive cell)与晶胞(cell)
- 晶格的基本重复单元称为晶胞。晶胞周期地铺展可以不交叠地覆盖整个晶格结构。其中,最小的晶胞取法称为初基原胞(primitive cell),简称原胞。
- 严格的说,原胞是晶体结构对应布拉维格子基本重复单元的最小取法。需要恰当选取基元,找到晶体结构的布拉维格子后,可以定义其原胞。原胞的一个操作定义是:由布拉维格子初基矢量所构造的平行六面体(三维)或平行四边形(二维)组成。原胞取法不唯一,但体积/面积确定,仅包含一个基元,是我们讨论布拉维格子的最小基本单位。
- 按照其他习惯选择称为惯用晶胞(conventional cell),含有多个基元,一般非最小单元。
- 对于体心立方、面心立方而言,惯用晶胞分别为包含2个和4个基元的立方体(见下面讨论),是将若干个基元视为一个复合“基元“时的”原胞“。
- 晶胞包含了结晶体的重要信息(原子种类、位置,对称性和平移矢量等等),是晶体结构的基本重复单元。考察具体材料的晶体结构,只需要考察其晶胞就可以了,对晶体学研究具有重要的意义。
-
二维晶格原胞举例
-
初基原胞
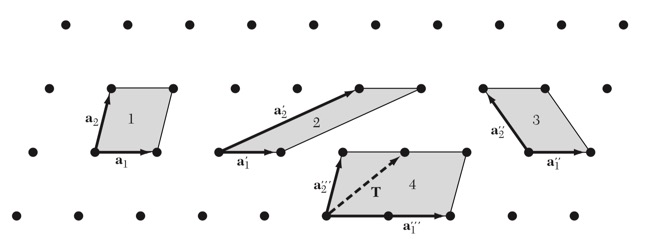
- (初基)原胞的选取不唯一,但面积相等,且仅包含一个基元(格点)。
- 问题:上图中哪几个是合法的元胞?哪几个不是?
-
惯用晶胞
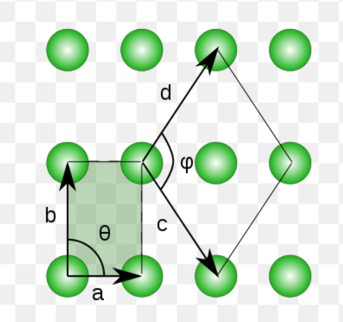
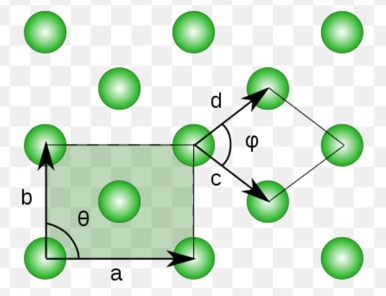
简单长方 有心长方 简单长方: $a,b$构成的平行四边形是最小原胞的一种选取方式,由$c,d$构成的平行四边形呢?(讨论)
有心长方: $a,b$构成的矩形是何种原胞?$c,d$呢?(讨论)
-
-
三维晶格原胞举例
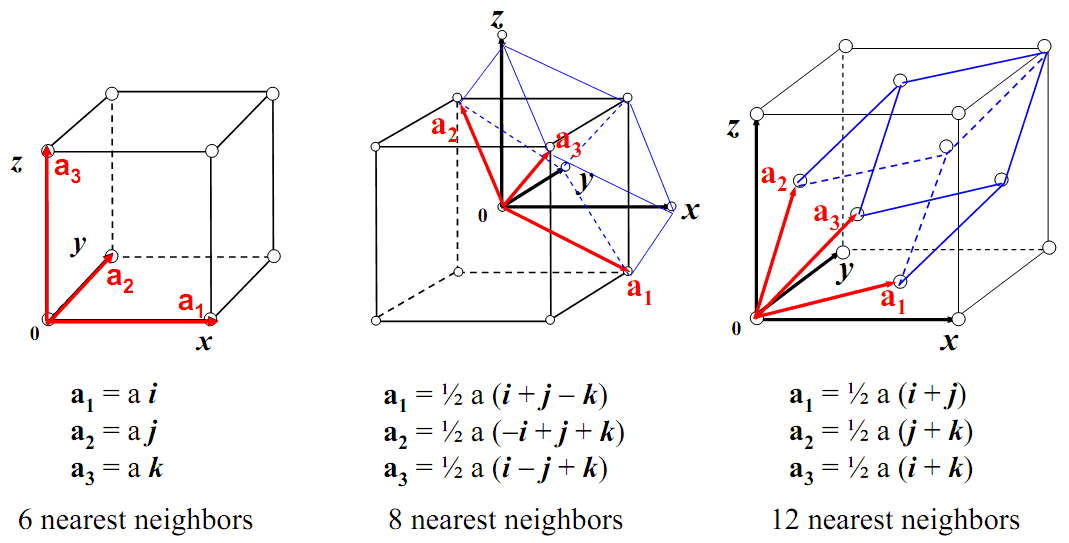
立方晶系三个成员(简单立方,体心立方与面心立方)的初基原胞和惯用晶胞 - 简单立方: 原胞为最小立方体。
- 体心立方: 原胞为$\bf{a}_1, \bf{a}_2, \bf{a}_3$构造的平行六面体;惯用晶胞为图示立方体。
- 面心立方: 原胞和惯用晶胞分别为何(讨论)。
- 问题: 体心立方和面心立方的原胞和惯用晶胞体积分别是多少?
-
魏格纳-赛兹原胞( Wigner-Seitz unit cell)
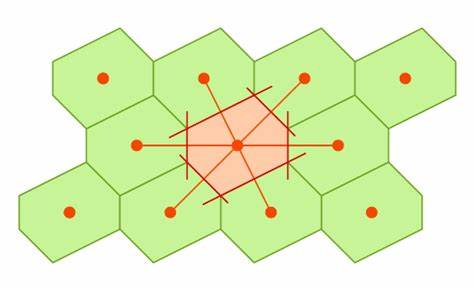
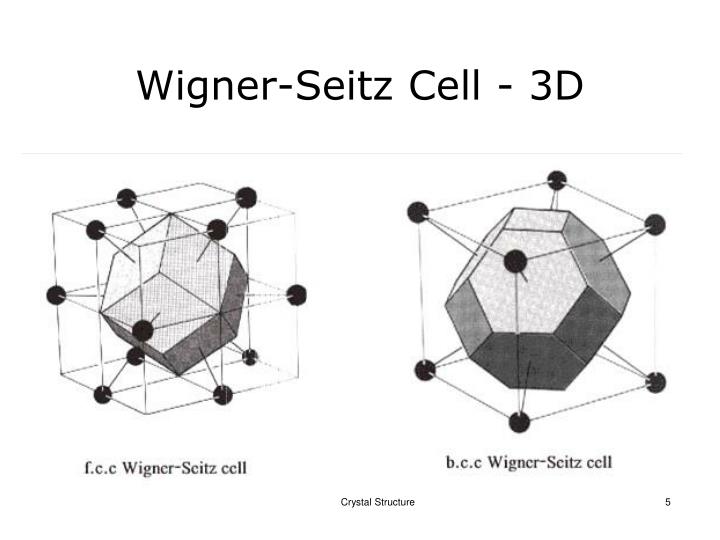
二维晶格的魏格纳赛兹原胞 三维晶格(面心立方和体心立方)的魏格纳赛兹原胞(正十二面体、截角八面体) -
魏格纳-赛兹原胞是这样的空间点的集合:即他们离布拉维格点R=0比离其他任何布拉维格点都近。
-
操作定义:被一个布拉维格点(原点)到其他所有格点所做的连线的平分线或平分面所包围的最小空间。
-
问题 :简单正方、简单立方格子的魏格纳-赛兹原胞是什么?
-
-
填充率计算(参见Sandro的视频讲义,以及喻舜尧同学的笔记)
- 布拉维格子:填充率=硬球的体积/原胞体积 (二维格子为面积比)
- 非布拉维格子:硬球体积需要乘以原胞中的硬球数目
- 重要数字:二维密堆积填充率三角格子最大($\frac{\sqrt{3} \pi}{6} \simeq$ 89%);三维的密堆积填充率为$\frac{\sqrt{2} \pi}{6} \simeq $ 74%。
4. 晶系分类与对称性
-
二维布拉维格子:4大晶系(crystal family)5种布拉维格子
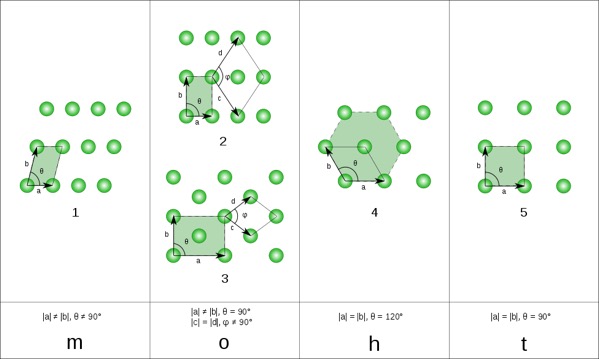
- 单斜晶系(monoclinic net):元胞为普通平行四边形
- 正交晶系(orthorhombic net):元胞为长方形,包含简单长方和面心长方两种
- 六角晶系(hexagonal net):元胞为菱形,初基矢量长度相等且夹60度(或120度)角
- 四角晶系(tetragonal net):元胞为正方形
-
三维布拉维格子:7大晶系,14种布拉维格子
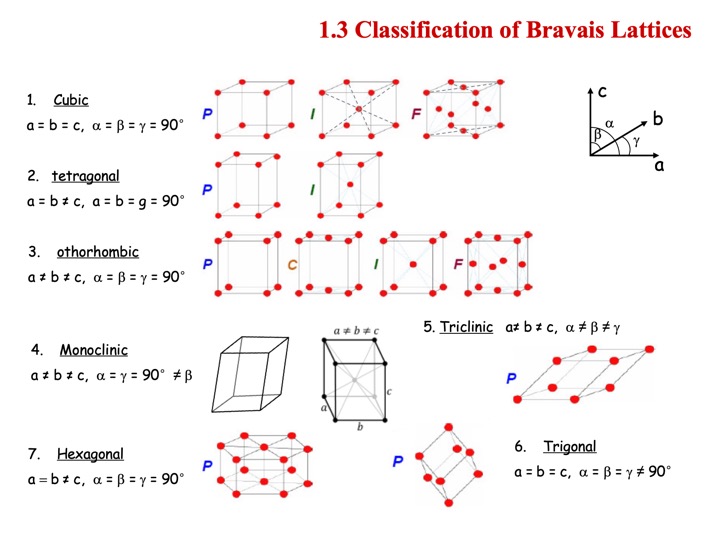
- 固体物理八卦一则:Frankenheim (1842) miscounted this number as 15, A. Bravais is the first one who gets a right counting (1845).
-
布拉维格子反映的是晶格的平移对称性
-
加上转动对称性,给出布拉维格子的分类。
-
转动轴只有1,2,3,4,6 五种(为何没有五度轴?)。
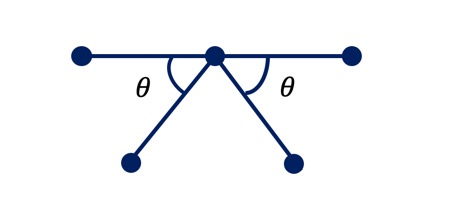
5度转动操作与平移对称不兼容(如何证明)
-
5. 晶向与晶面指数
-
布拉维格子中从某个格点(原点)指向另一个格点的矢量为晶向。互相平行的原子链称为晶向族[h,k,l],布拉维格子可以分解为晶向族(为什么?)。
-
布拉维格子可以分解为彼此平行、间距相等的晶面族。
-
定理: 三维布拉维格子的任意晶面均为二维布拉维格子。
因此三维布拉维格子可以被解理为二维布拉维晶面的堆砌。这些二维晶面按照不平行于晶面的晶格矢量“移动”,可以既不重复也不遗漏的覆盖整个三维晶格。
- 问: 是在三维布拉维格子中任意取三个不共线的格点形成的平面都可以作为晶面吗?
- 答: 是的。可以论证,三个格点间的两个格矢就一定会继续访问到无穷多的格点,并张开一个晶面,且此晶面必为二维布拉维格子。在这个面上任意取格点,通过三维布拉维格子的格矢可以访问任意格点,所此面扫过三维布拉维格子不会有遗漏。
-
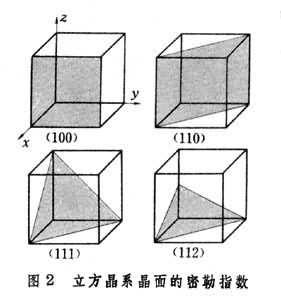
晶面指数操作定义: 选择某个布拉维格子为原点,同时选择一组初基矢量作为坐标轴,然后测量晶面族中任意一个成员(靠近原点为佳)在三个坐标轴上的截距$h,k,l$。则晶面指数为$(\frac{1}{h}, \frac{1}{k}, \frac{1}{l})$,为方便记,通常将三个分数通分后取整数。
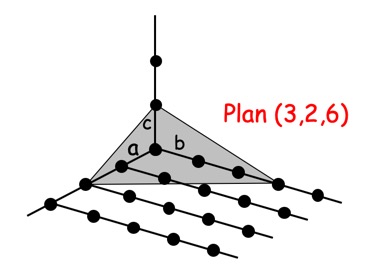
-
(1,0,0)晶面为平行于$y-z$平面的晶面,(1,0,0)与(0,1,0) ,(0,0,1)晶面等实质等价。(1,1,0)为平行$z$轴且与$x$,$y$轴各夹$\pm$45o的平行晶面族,依次类推。但是需要特别注意(1,1,2)晶面(如何证明其是一个合法的晶面编号?),与$z$轴截距处没有格点(即晶面指数的上述计算规则不必在坐标轴上切过格点)。
-
问题: 面心立方是哪个面堆叠起来形成密堆积结构的?(或者问,面心立方密堆面的晶面指数是什么)
-
对于体心立方和面心立方,通常不取初基矢量为轴,而是取惯用原胞的三个互相正交的$\hat{x}, \hat{y}, \hat{z} $ 方向为轴。这种对应惯用原胞取法的晶面指数称为米勒(Miller)指数。
-
延伸: 隐藏在操作定义背后的是引入与晶面垂直的法向方向来标记晶面。在引入倒格子(reciprocal lattice)的概念后,我们会证明晶面指数恰好定义了倒格子中的一族晶向,使得后者与晶面垂直。在立方晶系的情况下,倒格子的初基矢量与正格子相同,可以证明[h,k,l]晶向与(h,k,l)晶面垂直。
Slides & Video
-
Slides for Chapter 1 can be downloaded (please click the BIG icon below)
-
Video lectures (two, by Sandro Scandolo, ICTP), please click the icon below.
Discussions
- An online discussion (c.a. 30 + 30 min, via Wechat or Dingtalk) will be arranged.