第三章 晶体结合
Crystal Binding
 |
|---|
| 冰 — 氢键晶体 |
- 晶体依靠电磁相互作用结合,原子之间形成了能量较低的束缚态 — 化学键(bond),可以想象为”球棍模型“中的”棍“,连接着原子,形成稳定的晶体。在这一章,我们将对这些内容展开讨论。
1. 晶体的分类
-
在固体中,原子存在5种主要的结合形式:分子键、离子键、共价键、金属键、和氢键。可以按照化学键的形式将晶体进行分类。
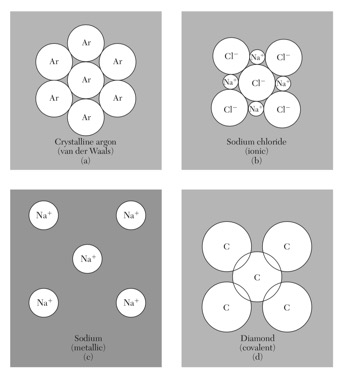
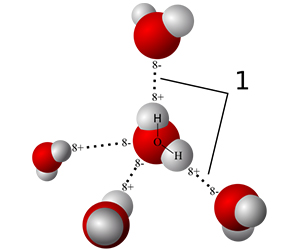
晶体的分类(四类主要化学键) 特殊的结合方式—氢键 不同结合方式(键)有不同具体机理:分子键主要通过范德瓦尔斯相互(瞬时偶极-偶极)作用,离子键通过正负离子间的库伦作用,共价键通过电子云交叠产生交换相互作用等。
-
结合能:将固体拆分成电中性、相距无穷远的自由原子集合,所需要的能量称为结合能。不同的化学键类型,结合能不同。通常共价键、金属键、离子键较强,而分子键一般较弱。
-
实际晶体中可以存在不止一种化学键,例如石墨中存在共价键(层内)和分子键(层间范德瓦尔斯相互作用),冰中同时存在共价键和氢键。
2. 范德瓦尔斯晶体
-
常温下的惰性气体He、Ne、Ar、Xe等,在低温下依靠范德瓦尔斯力结合成范德瓦尔斯晶体(H2 和 O2等形成晶体时也称为分子晶体)。惰性气体原子中的电子处于满壳层结构,呈现电中性,但可以通过瞬时电偶极矩相互作用,通过量子力学机制发生相互耦合。
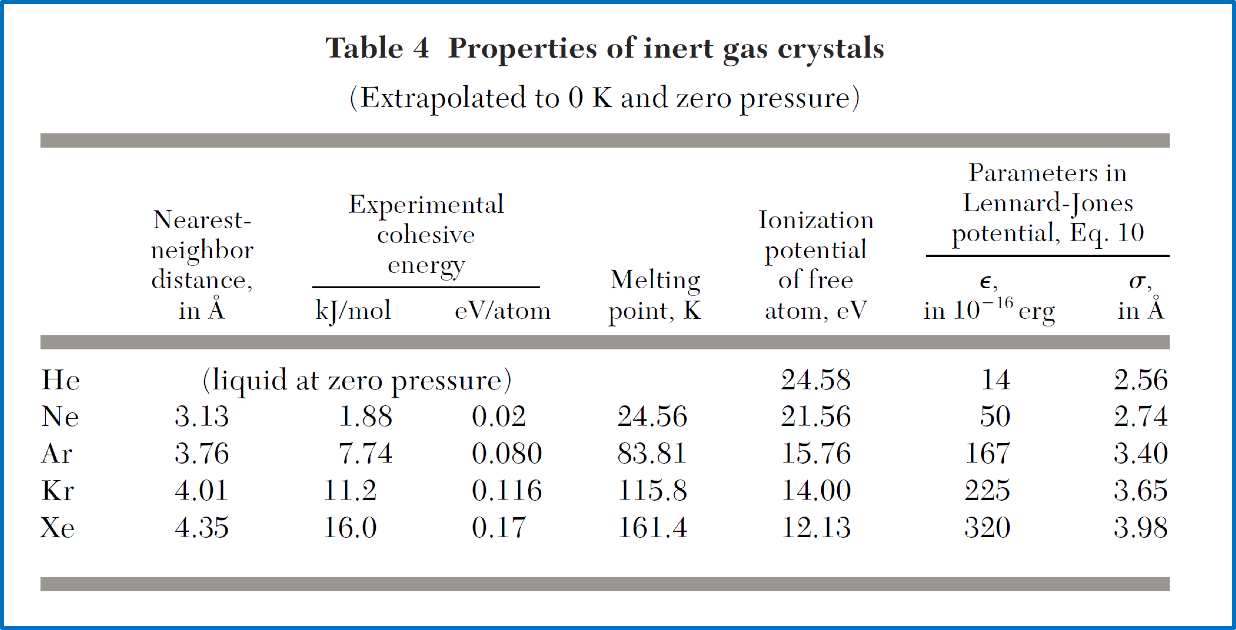
惰性原子的范德瓦尔斯晶体 -
范德瓦尔斯相互作用
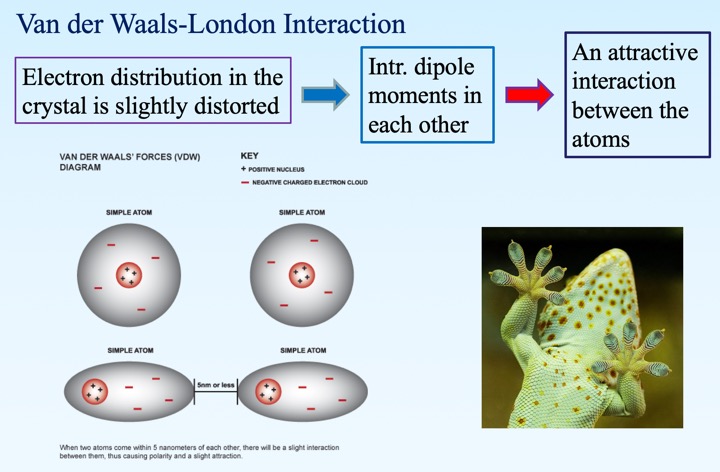
范德瓦尔斯力的瞬时产生机制。瓦德瓦尔斯相互作用非常普遍,在生物现象中也存在,例如壁虎的爪子。 -
偶极相互作用的理想模型
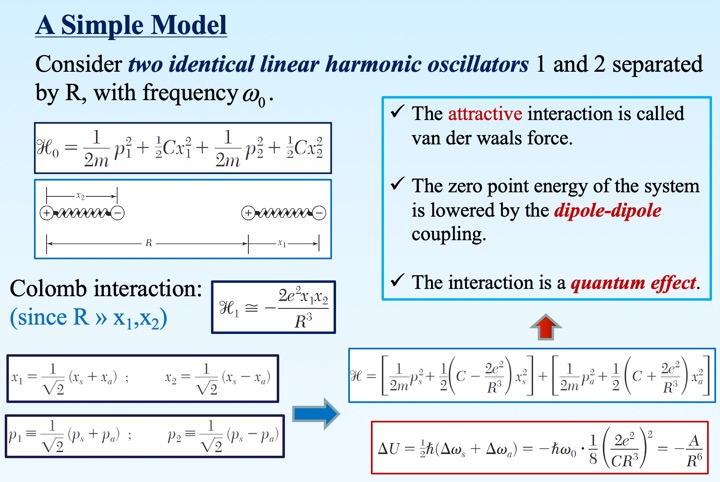
按照理想模型,采取简正坐标对角化双耦合谐振子模型,解耦得到两个有效简正模式$x_a$,$x_s$。从而得到低于未耦合谐振子的零点能量(吸引相互作用),且相互作用势与谐振子之间距离R的6次方成反比(下降)。 -
范德瓦尔斯相互作用为电中性原子的各向同性相互作用,因此晶体多采取紧密排列的形式,上面所述的惰性原子范德瓦尔斯晶体均为面心立方结构。

范德瓦尔斯晶体的面心立方密堆积结构 -
勒纳德-琼斯势
原子之间除了存在与距离$1/R^6$的范德瓦尔斯吸引相互作用之外,当原子足够靠近时还应存在排斥相互作用,以稳定晶体避免坍缩。
-
泡利不相容原理与排斥相互作用:当A、B两个原子逐渐接近时,原子轨道上的电子云会发生交叠,A原子轨道上的电子会有一定概率占据B原子对应轨道上。然而,由于原子为封闭壳层结构,B原子对应轨道上已经占据了电子,而一个指定量子数的轨道上不能扎占据超过1个电子。这就是泡利不相容原理,会导致如惰性气体原子等饱和壳层结构的原子/分子互相接近到一定程度时由于电子云交叠产生排斥相互作用。
-
唯象的,人们提出一个与距离$R$的12次方成反比的排斥相互作用。注意,排斥相互作用比吸引势随距离增长衰减快,并随距离减小迅速增长。
-
将两部分相互作用合起来,我们得到著名的勒纳德—琼斯势
$U(R) = 4 \epsilon[ (\frac{\sigma}{R})^{12} -(\frac{\sigma}{R})^6 ] $
有时也简记 $A = 4 \epsilon \sigma^{12}$,$B = 4 \epsilon \sigma^{6}$。
-
勒纳德—琼斯势保证了两个原子在距离近时互相排斥,距离远时互相吸引,存在一定的平衡位置。在平衡位置处,晶体总势能为负,其绝对值即结合能。
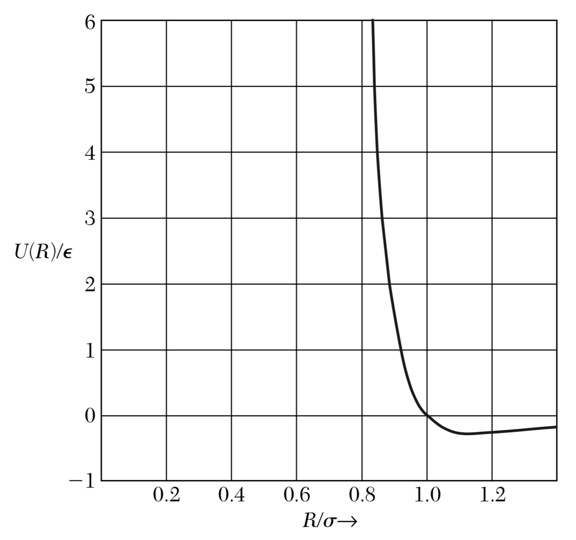
勒纳德—琼斯势:存在平衡位置$R_0\simeq 1.12 \sigma$处*(如何证明?作业)*,平衡位置左边(短距离)曲线上升陡峭,迅速变为正值;右边(长距离)则变化相对平缓,逐渐趋向0能。
-
3. 共价键晶体
-
与范德瓦尔斯键不同,共价键是一种很强的化学键,在金刚石、硅、锗等单质,各种有机化合物中十分常见。
-
共价键的三个特征:饱和性(电子配对),方向性(轨道相关)。
-
最简单的共价键:氢分子中两个原子之间共享一对电子形成共价键。
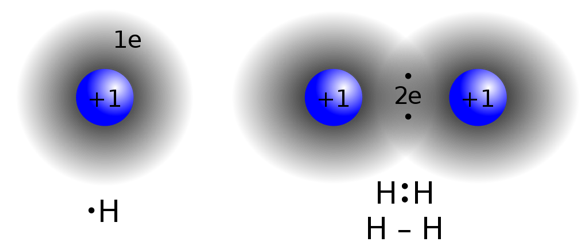
氢分子中的两个原子各自贡献一个电子,形成共价键,在键中心区域电子密度高,形成键合,将两个氢原子束缚在一起形成分子。 -
分子轨道理论:形成共价键的两个电子不再围绕各自的原子核运动(原子轨道),而是在二者的组合—分子轨道上运动。不难知道这样的分子轨道有两个(成键与反键):
$\psi_a(r_1,r_2) = \phi_1(r_1) \phi_2(r_2) - \phi_1(r_2) \phi_2(r_1)$
$\psi_s(r_1,r_2) = \phi_1(r_1) \phi_2(r_2) + \phi_1(r_2) \phi_2(r_1)$
(问: $\psi_a$与$\psi_s$哪个是成键轨道,哪个是反键?)
-
对应于对称与反对称空间轨道部分,需要有反对称(singlet)与对称(triplet)自旋部分与之相乘,使得整个双电子波函数满足费米-狄拉克统计。
-
一个有趣的联系——量子磁性:看起来共价键成键与反键的能量差取决于自旋形成单态还是三重态,因此两个轨道能量可以形式上写成 $J S_1 \cdot S_2$,称为自旋交换积分$J = \Delta E$,而$\Delta E$为成键轨道与反键轨道能量差。事实上正是这“自旋-自旋耦合”导致了磁性的产生(磁性的本质起源为量子力学的)。
-
-
sp3杂化与正四面体键:金刚石结构的C-C化学键
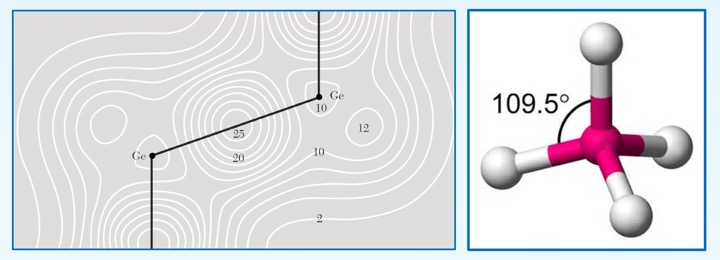
金刚石结构(锗)的电子密度与四面体键 -
C原子的外层电子排布:
1s 2s 2p 2p $\uparrow \downarrow$ $\uparrow \downarrow$ $\uparrow$ $\uparrow$ -
不难看到,C原子外层只有两个未配对电子(2p),为了实现与附近4个原子形成共价键,首先发生一次sp3杂化,电子排布变为:
1s sp3 sp3 sp3 sp3 $\uparrow \downarrow$ $\uparrow$ $\uparrow$ $\uparrow$ $\uparrow$ 其中sp3轨道为
$h_1 = \frac{1}{2} (| s \rangle + | p_x \rangle + | p_y \rangle + | p_z \rangle)$
$h_2 = \frac{1}{2} (| s \rangle + | p_x \rangle - | p_y \rangle - | p_z \rangle)$
$h_3 = \frac{1}{2} (| s \rangle - | p_x \rangle + | p_y \rangle - | p_z \rangle)$
$h_4 = \frac{1}{2} (| s \rangle - | p_x \rangle - | p_y \rangle + | p_z \rangle)$
(作业:证明四个轨道正交归一)
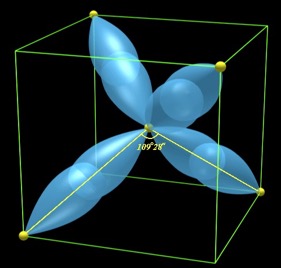
sp3 杂化轨道 -
虽然发生sp3需要“消耗”一些能量,然而由于多形成了2个共价键,完全可以“补偿”这部分损失,并获得很大的晶体结合能(金刚石中高达7.4 eV!)。
-
对于上面讨论的H-H,C-C共价键,电子处于键中央的对称位置,共价键为非极性的;然而,对于两个原子电负性(吸收一个电子释放出的能量)不同时,共价键具有极性。当电负性差异很大时,从需要使用量子力学计算的共价键结合方式连续过渡到准经典的离子键。
-
4. 离子键晶体
-
NaCl,CsCl等电负性很强的卤族元素与容易丢失电子的金属元素结合,可以采用半经典理论直接处理,即离子键。
-
金属原子丢失电子,卤族俘获电子,阴离子与阳离子都形成满壳层结构,但是分别带正负电荷,在此过程中存在离子化能量(由中性原子变为离子)。再将离子从无穷远处移动到晶格上,可以按照经典静电场计算结合能。
-
设离子间的平衡位置间距为$R$,且离子所带电荷为$\pm q$,则所有其他格点$j$对格点$i$处离子的静电能(称为马德隆能)为$U_{i} = \sum_j \pm \frac{1}{p_{ij}} \frac{q^2}{R}$,$p_{ij}$为$j$处离子到$i$处离子的距离(以$R$为单位)。
-
定义马德隆常数 $\alpha = \sum_j^{'} \pm \frac{1}{p_{ij}}$,则马德隆能为$U_i=\alpha \frac{q^2}{R}$。
-
马德隆常数计算:
-
一维情况:$\alpha = 2 (1-1/2+1/3-1/4 + …) = 2\ln{2}$

一维离子晶体 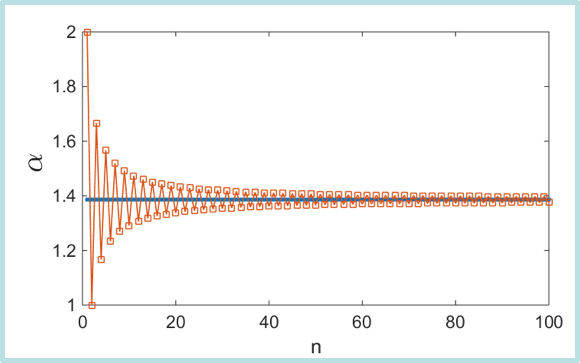
马德隆常数的数值结果 -
三维情况(NaCl为例)
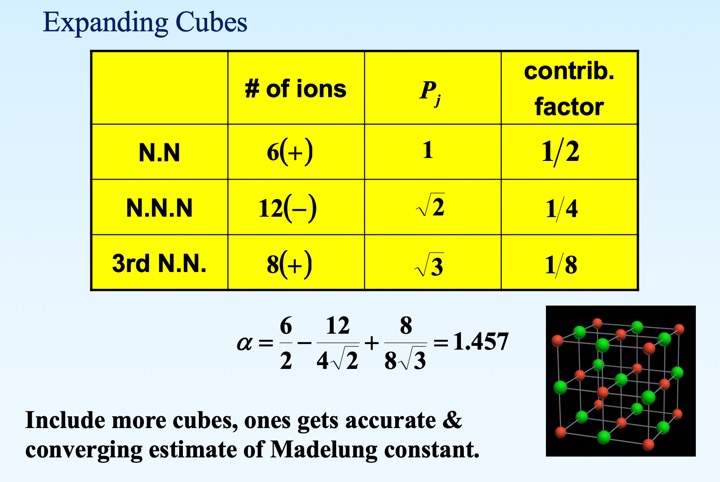
-
-
离子键是一种强键合,离子晶体熔点高,硬度强。
5. 金属键晶体
- 金属中带负电的电子云自由运动,充当媒介,将阳离子键合起来。
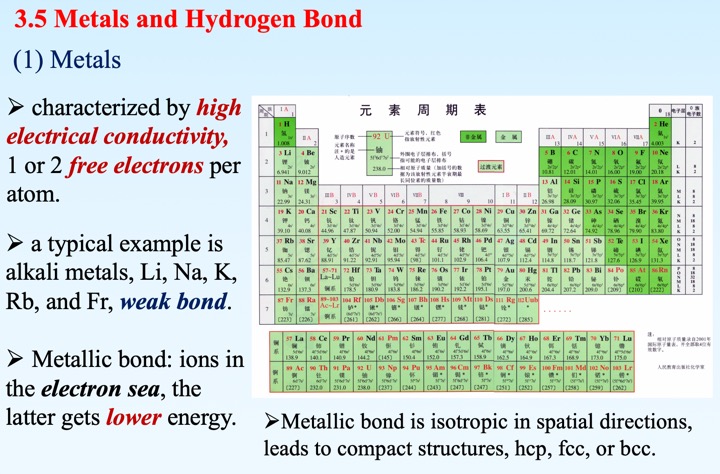
6. 氢键晶体
- 氢原子中的电子几乎被氧原子俘获,质子“裸露”在外,与另一个靠近的氧离子发生静电吸引,称为氢键。
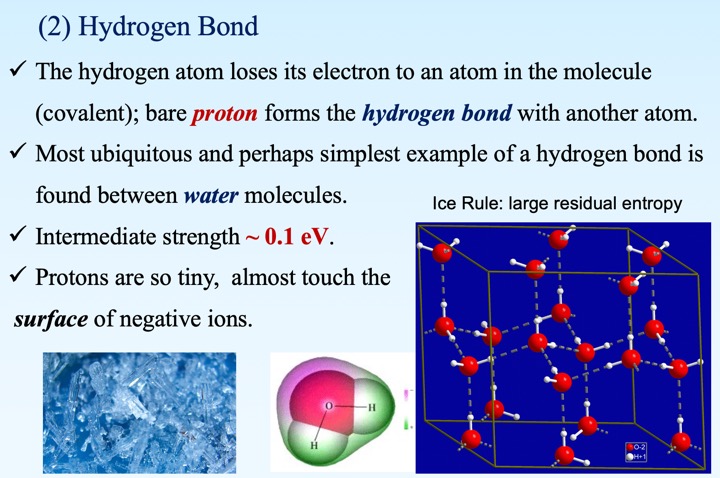
- 冰中的氢与氧形成共价键或氢键的选择具有一定随机性,但需要保证每一个氧所对应的4个键中2个为共价键,2个为氢键(2进2出),称为冰规则。
- 由于具有宏观大的简并度,冰即便降至零温度,也存在非零的均格点熵,称为零温熵。
Slides & Video
-
Video lectures (two, by Sandro Scandolo, ICTP), please click the icon below.
Discussions
- An online discussion (c.a. 90 min, via Wechat or Dingtalk) will be arranged.
Homework
-
根据勒纳德-琼斯势,计算平衡位置$R_0$,以及结合能$U(R_0)$的表达式。
-
为维持NaCl晶体稳定,除静电吸引相互作用之外,需在最近邻离子之间引入排斥相互作用,有两种引入方式: (a) $\lambda e^{-R/\rho}$($\rho$为特征长度)或 (b) $B/R^n$($B$为某常数,$n$为某正整数)。假设马德隆常数为$\alpha$,请考虑(a)和(b)两种不同的排斥势,写下平衡位置$R_0$需要满足的方程,并计算在平衡位置处的马德隆能。
-
估算(a)二维正方格子,(b)六角格子上的马德隆常数。
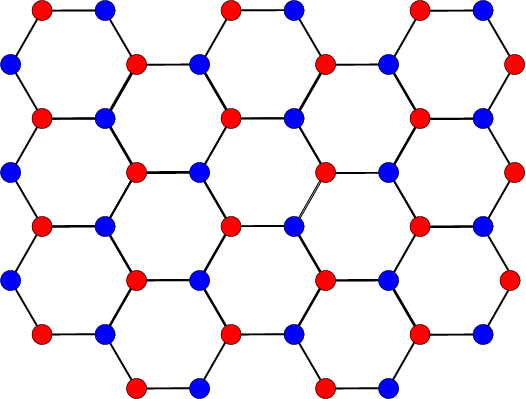
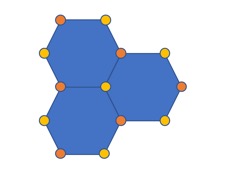
(a) 六角格子,蓝色和红色分别代表两种离子占据位置。 (b) 采用上述晶胞估算马德隆常数
[assigned: 20-March-2020, due: 27-March-2020]
