第四章 晶格振动
Crystal Vibration
 |
|---|
| Atoms are in a perpetual movement in solids |
| “静止是相对的,运动是绝对的。“ ——运动是物质的存在方式与固有属性。哲学上说的运动是一般的、抽象的,但是马克思主义哲学的这个著名论断在描述晶格上发生的物理时,却是再合适不过了。 |
-
尽管晶体中的原子有序排列成近乎完美的晶格结构,但我们不能将其简单地视为静止的纯几何结构,而是要需要考虑其运动,才能理解固体的一些重要性质,如固体比热的低温反常、晶格的热输运、超导BCS理论等。
-
在热运动、外界扰动等影响下,晶格上的原子总是会在平衡位置附近运动,并形成一定的集体运动模式——晶格振动,并在系统中激发产生一种准粒子——声子。
-
场与准粒子
-
量子化场的波动和准粒子激发可以联系起来。在理想的情况下,场的统计问题可以被简化成准粒子自由气体的统计问题。
-
晶格振动与声子激发是一个多自由度的量子场论问题。我们也必须使用量子的理论才能够理解固体中晶格振动的性质。
-
”两朵乌云“:“第二朵乌云出现在关于能量均分的麦克斯韦-玻尔兹曼理论上”。第二朵乌云导致量子论的诞生,他有2个具体所指,一个是大家熟知的(光子气)黑体辐射,另一个是我们即将讨论的(声子气)固体比热。能均分定理将在讨论后者的低温热力学性质中失效。这两个例子有非常多类似之处。
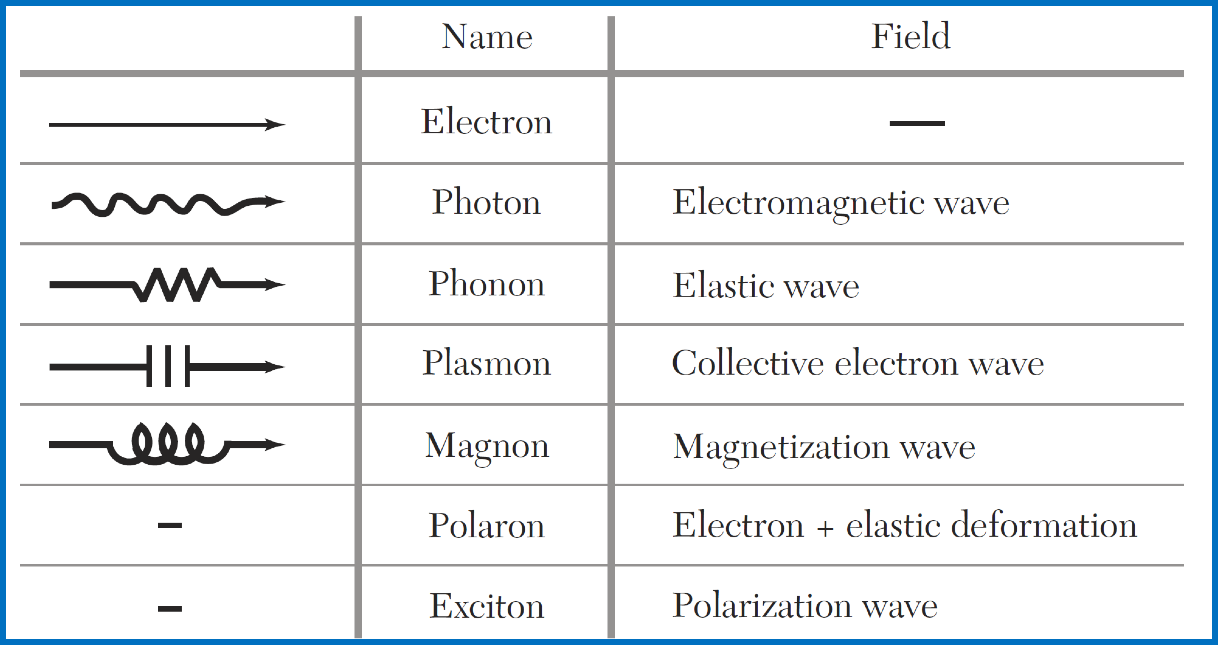
量子场与准粒子 -
1. 一维原子链模型
-
三维晶格振动的纵波与横波(波矢K垂直原子面)
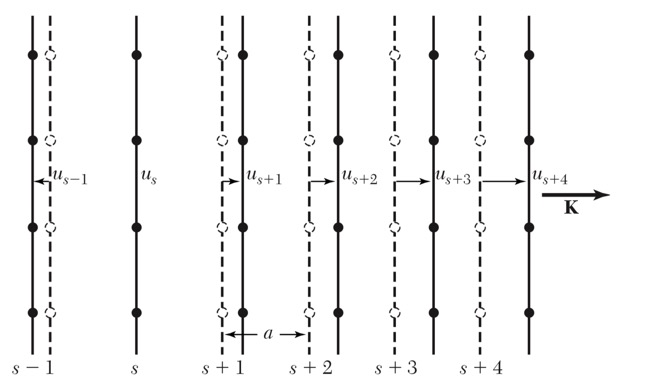
三维晶格振动的纵波:原子运动平行于K 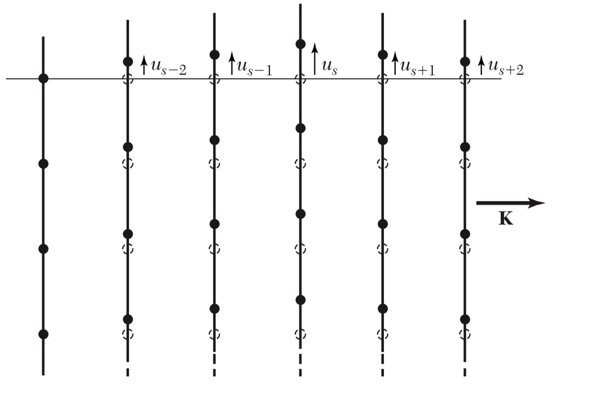
横波振动:原子运动垂直于K -
将晶格振动简化为下面的一维模型
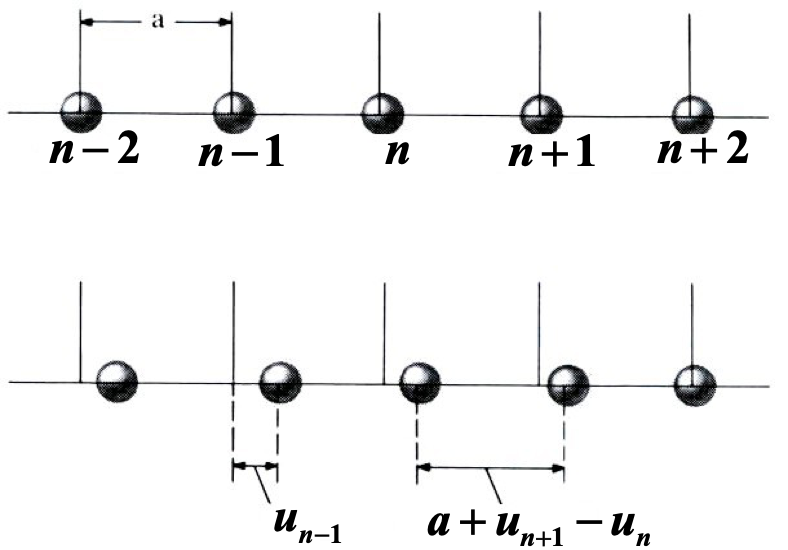
一维原子链的耦合谐振子模型:(上图)原子处于平衡位置,晶格常数为$a$;(下图)偏离平衡位置的原子位形。假设第$n$个原子偏离平衡位置的矢量为$u_n$ ,在一维情况下$u_n$为一个可取正负值的标量,约定为向右为正,向左为负)。两个相邻原子$n$和$n+1$的间距为$u_{n+1}-u_{n}$。 -
简谐近似: 两个相邻原子间的相互作用势能为$\phi(x)$,$x$为原子间距,固体中$x=a+\delta$,$\delta$为一小量。势能可以展开为:
$\phi(a+\delta) = \phi(a) + \frac{d \phi(x)}{d x}|{x=a} \delta + \frac{1}{2!} \frac{d^2 \phi(x)}{d x^2}|{x=a} \delta^2 + …$
由于$\phi(a)$为势能极小点(不失一般性,取$\phi(a)=0$),$\frac{d \phi(x)}{d x}|_{x=a}=0$。
按照简谐近似取到2阶项,并简记弹性系数$\beta \equiv \frac{d^2 \phi(x)}{d x^2}|_{x=a}$。
-
弹性势能为:$\phi(\delta) = \frac{1}{2} \beta \delta^2$
-
弹性力为$f = -\frac{d\phi}{d\delta} = -\beta \delta$
-
2. 格波
-
晶格振动运动方程与波动解

$N$个相互耦合的谐振子,格波在其中传播。 仅考虑最近邻相互作用,$N$个原子的耦合运动方程,对于第$n$个原子而言:
$\beta(u_{n+1}-u_n) - \beta(u_{n}-u_{n-1})= M \frac{du_n^2}{dt^2}$
$M$为原子质量。
-
为求解$N$个原子的耦合方程组,引入傅里叶变化,得到方程组的解为:
$u_n(t) = A e^{i (q na - \omega t)}$,其中$A$为振幅,$\omega$为圆频率,$q$为波矢,是代表波的传播模式。
-
代入运动方程,可以得到能动关系为:
$\omega^2(q) = \frac{2\beta}{M} (1-\cos{qa})$
$\omega(q) =2 \sqrt{\frac{\beta}{M}} |\sin{\frac{qa}{2}}|$
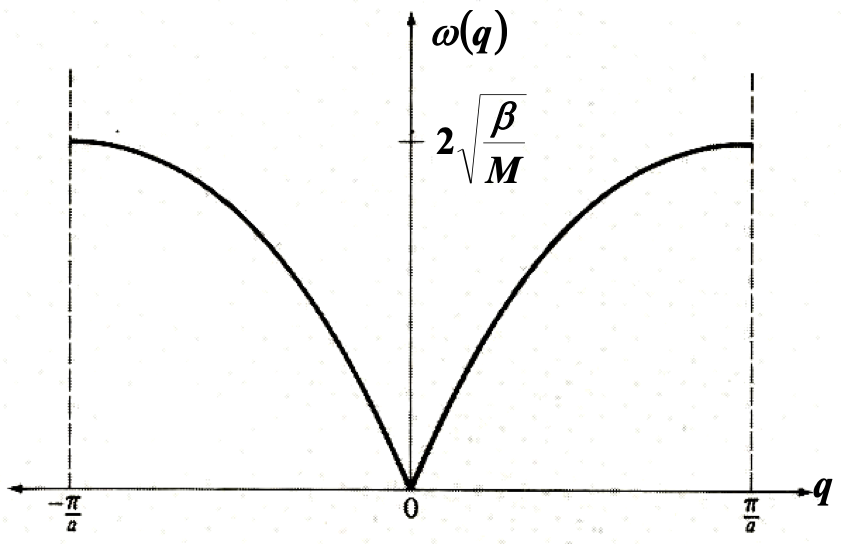
一维原子链格波的 $\omega$ - $q$ 色散关系。 -
长波极限: $q$趋近于0,$\omega(q) \simeq \sqrt{\frac{\beta}{M}} qa$,线性色散。
-
在无穷长的热力学极限下,$q$可以连续的取值。但是为了方便处理,下面指出,有限尺寸系统的格波波矢$q$的取值有一定的要求。另外,在连续空间中,$q$可以从0取到无穷,但作为分立格点系统上的波矢$q$有一些特殊性。
-
-
波恩—冯卡曼边界条件

为了处理问题方便,固体物理中常常采用具有周期边界条件的环(也称为波恩—冯卡曼边界条件),使得有限尺寸系统也具有了平移不变性和波数$q$。周期边界条件看似”不物理“,但是在热力学极限下($N \to \infty$),边界项对体态性质带来的影响不甚重要。 周期边界条件对固体中许可的波矢提出了限制条件,即:
$e^{iq na} = e^{i q (n+N)a}$,因此$q Na = 2 m \pi $
因此波矢取一系列分立值,$q = m \frac{2\pi}{Na}$,$m$为整数。
-
等价波矢与布里渊区
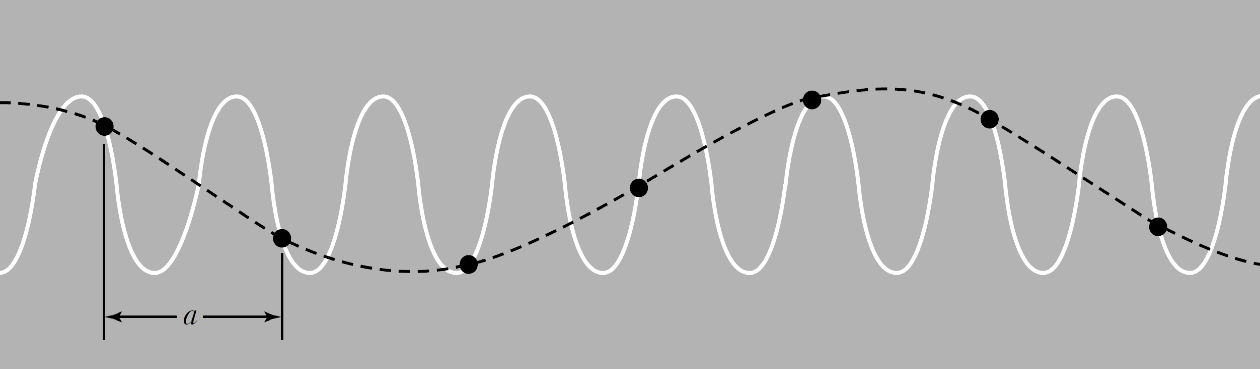
上述两个格波波矢为 $q_1=\frac{2\pi}{5a}$(对应波长$\lambda=5a$)和波矢 $q_2=\frac{12\pi}{5a}$ (对应波长为$\frac{5}{6}a$),对于分立晶格系统,两个波矢 $q_1$ 和 $q_2$ 没有 区别。 -
对于晶体系统,波矢 $q$ 与 $q+G$ 为等价波矢,其中 $G= m \frac{2\pi}{a}$ 为倒格矢。
- 格点位移 $u_n = Ae^{i(q+G) na} = Ae^{iq na}$。
- 色散关系 $\omega(q+G) = 2 \sqrt{\frac{\beta}{M}} |\sin{(\frac{qa}{2}+\frac{Ga}{2})}| =\omega(q) $
-
考虑到原子位移和色散关系等晶格振动对 $q$ 的周期性,因此可以选取区间 $q \in [-\pi/a, \pi/a]$ 内的点来代表所有运动模式,称为布里渊区。
-
在第一布里渊区内存在振动模式数目为 $\frac{2\pi/a}{2\pi/Na} = N$ ,与格点数目相等。无论是数实空间变量数目 ${u_n}$ 还是 $q$ 空间振动模式,总自由度不变。
-
在布里渊区边界上 $q= \pm \pi/a$,$u_n= e^{i q na} = e^{i n \pi} = (-1)^n$,代表正向与反向传播叠加的驻波解。
-
按照入射波垂直晶面,$\theta=\pi/2$,布里渊区边界的点发生格波的布拉格反射。
$2a \sin(\theta) = \lambda = 2a$。
-
-
3. 双原子链:声学支与光学支
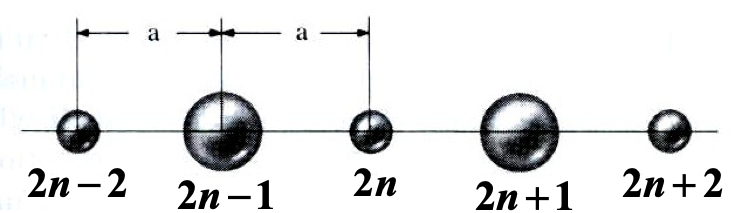 |
|---|
| 双原子链系统,晶胞中包含两个不同质量的原子$M$和$m$,弹性系数为$\beta$,晶格常数为$2a$。 |
-
双原子链中,奇数格点上 $M$ 的位移标记为 $u_{2n-1}, u_{2n+1}, u_{2n+3}, …$;而偶数格点上 $m$ 的位移标记为 $u_{2n-2}, u_{2n}, u_{2n+2}, …$。
-
采取简谐近似,列出双原子链的$2N$个运动方程(Equation of Motion, EoM)
$m \frac{d^2 u_{2n}}{d t^2} = \beta (u_{2n+1}+u_{2n-1}-2u_{2n})$
$m \frac{d^2 u_{2n+1}}{d t^2} = \beta (u_{2n+2}+u_{2n}-2u_{2n+1})$
-
代入两个原子的位移波函数
$u_{2n} = Ae^{i[q(2n)a - \omega t]}$
$u_{2n+1} = Be^{i[q (2n+1)a - \omega t]}$
得到需要求解的方程组$X (A, B)^T = 0$,其中$X$矩阵为
$ 2\beta - m \omega^2 $ $- 2 \beta \cos(qa) $ $ -2 \beta \cos(qa) $ $ 2\beta - M \omega^2 $ 令$|X| = 0$,得到本征运动模式和色散关系如下:
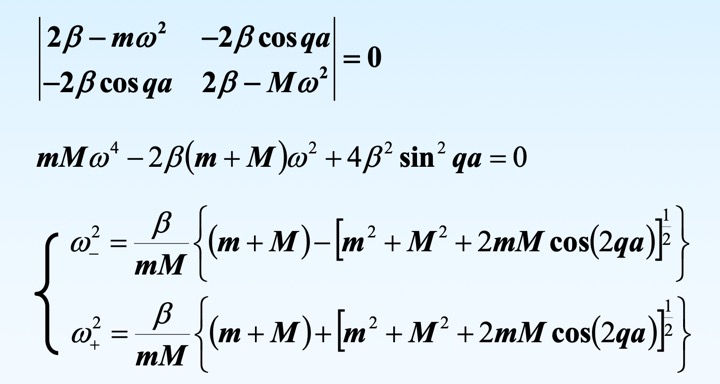
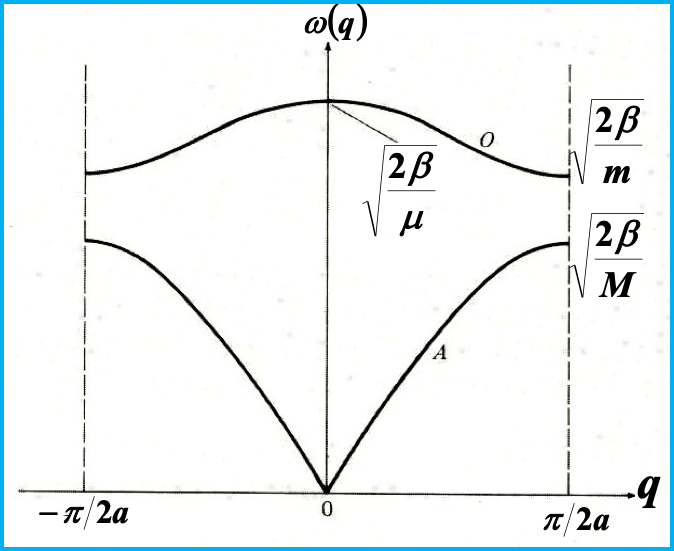
久期方程 色散关系,存在两支解,分别称为光学支和声学支 -
布里渊区,振动模式数,等价 $q$ 点
-
按照波恩-冯卡曼边界条件,第一布里渊区范围为:$q \in [-\frac{\pi}{2a}, \frac{\pi}{2a}]$,波矢最小间距为 $\frac{2\pi}{2Na}$,每支激发上的 $q$ 点数目为 $(\frac{\pi}{a})/(\frac{\pi}{Na}) = N$,两支激发共计 $2N$ 振动模式,与双原子链自由度吻合。
-
按照 $G= \frac{2\pi}{2a}$,因为 $\cos[2(q+G) a] = \cos[2(q+\frac{\pi}{a}) a] = \cos(2qa)$
可以得到 $\omega_{\pm}(q+G) = \omega_{\pm}(q)$。
-
-
长波极限
取$q\to 0$的长波极限,对色散关系进行分析:

声学支: 零能激发无能隙,线性色散。 
光学支:长波光学支激发能隙 $\sqrt{\frac{2\beta}{\mu}}$,$\mu = \frac{mM}{m+M}$ -
长波声学支图像
求解久期方程得到本征能量后,可以求得振幅$A,B$的比值
$A/B = [ 2\beta - M \omega^2 ]/[2 \beta \cos(qa)]$
在长波声学支解中,取$q\to 0$(同时$\omega \to 0$):
$A/B \simeq 1$
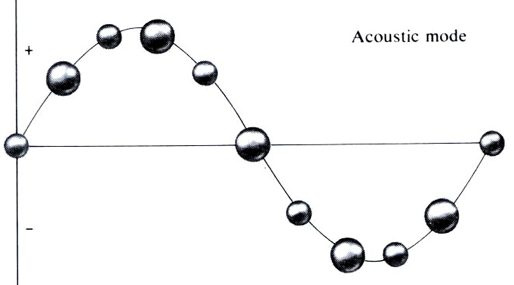
双原子质心做类似单原子链运动 -
长波光学支图像
$A/B \simeq [2\beta - M \frac{2 \beta}{mM} (M+m)]/2\beta = -\frac{m}{M}$
因此光学支长波振动中质心不动:$A M + B m = 0$。
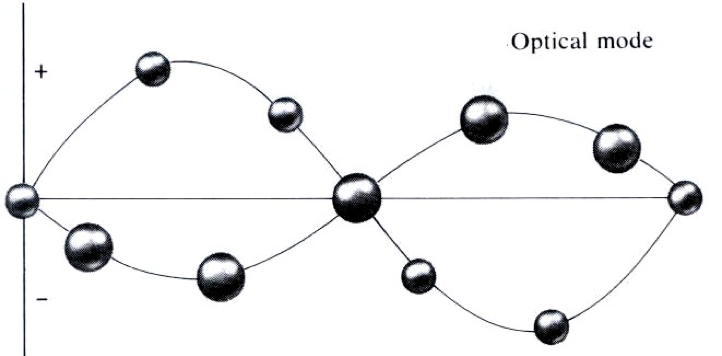
双原子围绕质心振动,容易被电磁波激发
-
4. 简正模式与格波量子化
通过上面的讨论,我们知道晶格振动可以化为一系列正交归一完备的平面波的叠加。因此,我们可以把描述从实空间原子坐标$u_n$转换为广义坐标——波函数分量的振幅$A_q$。
-
第$n$个原子的位移$u_n$可以展开成
$u_n = \sum_q A_q e^{i(qna - \omega_q t)} + A_q^* e^{-i(qna - \omega_q t)} = \frac{1}{\sqrt{N}} \sum_q a_q e^{iqna} + a_q^* e^{-iqna}$
其中坐标 $a_q = \sqrt{N} A_a e^{-i\omega_q t}, a_q^* = \sqrt{N} A_a^* e^{i\omega_q t}$。
-
格波的动能为
$T = \frac{M}{2} \sum_{n=1}^N \dot{u}_n \dot{u}_n$
将$u_n$用$a_q$表达,得到:
$T = \frac{M}{2N} \sum_{n=1}^N (\sum_q \dot{a}_q e^{iqna} + \dot{a}_q^* e^{-iqna})(\sum_q \dot{a}_q e^{iqna} + \dot{a}_q^* e^{-iqna})$
并考虑到$\dot{a}_q = -i \omega_q a_q$
$T = \frac{M}{2} \sum_q \omega_q^2 (2a_q a_q^* -a_q a_{-q} -a_q^* a_{-q}^*)$。
-
原子势能项为
$V = \frac{\beta}{2} \sum_n (u_{n}-u_{n-1}) (u_{n}-u_{n-1}) = \frac{M}{2} \sum_q \omega_q^2 (2a_q a_q^* +a_q a_{-q} + a_q^* a_{-q}^*) $
其中使用了 $\frac{\beta}{2} (2-e^{iqa}-e^{-iqa}) = \beta [1-cos(qa)] =2 \beta \sin^2{\frac{qa}{2}} = \frac{M}{2} \omega_q^2$
-
哈密顿量
$H = T + V = M \sum_q \omega_q^2 (a_q a_q^* + a_q^* a_q)$
-
引入(实)简正坐标 $x_q$与共轭动量$p_q$
$x_q = a_q + a_q^*$
$p_q = \frac{M\omega_q}{i} (a_q - a_q^*)$
其逆变换为
$a_q = \frac{1}{2} (x_q + \frac{i}{M\omega_q} p_q)$
$a_q^* = \frac{1}{2} (x_q - \frac{i}{M\omega_q} p_q)$
-
使用简正坐标,可以将哈密顿量表达为简正模式之和
$H = \frac{M}{2} \sum_q \omega_q^2 (x_q^2 + \frac{1}{M^2 \omega^2} p^2_q) = \sum_q \frac{M}{2} \omega_q^2 x_q^2 + \frac{p^2_q}{2M}$
-
简正模式量子化与声子
系统的总哈密顿量 $H = \sum_q H_q$,其中$H_q = \frac{M}{2} \omega_q^2 x_q^2 + \frac{p^2_q}{2M}$,即解耦的谐振子——简正模式。
量子化: 将每个简正模式$H_q$量子化,即量子谐振子。引入阶梯算符$a,a^\dagger$,则谐振子可以写作
$a_q = \sqrt{\frac{M \omega}{2\hbar}} (x_q + \frac{i}{M\omega_q} p_q)$
$a^\dagger_q = \sqrt{\frac{M \omega}{2\hbar}} (x_q - \frac{i}{M\omega_q} p_q)$
验证$[a_q, a^\dagger_{q'}] = \delta_{q,q'}$
$H_q = \hbar \omega_q a_q a^\dagger_q = \hbar \omega_q (n_q + 1/2)$,其中$n_q = a_q^\dagger a_q$表示简正模式处在第$n_q$个激发态。
声子: 简正模式$\omega_q$处于第$n_q$个激发态则激发$n_q$个声子。则晶格振动可以表达为$q$-模式激发$n_q$个声子的集合(无相互作用声子气)。注意,$q$-模式所激发的声子不是某个原子的个别激发带来的,而是所有$N$个原子的集体激发。
5. 长波极限下的一维自由玻色场
上面介绍的是分立情况下的量子化过程。在有些情况下,先取连续极限,写成经典场然后将其做正则量子化的过程,推导更为简明、系统,下面介绍这部分内容。
-
先写下晶格振动的拉格朗日量:
$L = T - V = \sum_{n=1}^{N} \frac{m \dot{u}_n^2}{2} - \frac{\beta}{2} (u_{n+1} - u_n)^2$
-
从凝聚态物理的现代视角,我们特别关心系统的低能激发,在晶格振动问题上,这对应着长波极限,因此我们取连续极限将分立$u_n$映射成经典连续场$\phi(x)$,其中:
$u_n \rightarrow a^{1/2} \phi(x)$,其中$1/2$为标度维度(scaling dimension)
$u_{n+1} - u_n \rightarrow a^{3/2} \partial_x \phi$,标度维度为$3/2$
$\sum_n \rightarrow \frac{1}{a} \int_0^L dx$,其中 $L = Na$
-
拉氏量:$L = \int_{0}^{L} \mathcal{L}(\phi, \partial_x \phi, \dot{\phi}) dx $,其中 $\mathcal{L}(\phi, \partial_x \phi, \dot{\phi}) = \frac{m}{2} \dot{\phi}^2 - \frac{\beta a^2}{2} (\partial_x \phi)^2$ 为拉氏密度。
-
经典场论
-
作用量$S[\phi] = \int dt \int dx \mathcal{L}(\phi, \partial_x \phi, \dot{\phi})$
-
作用量极小原理 $\delta S[\phi] = 0$可以推导出拉式运动方程:
$\phi(x,t) \rightarrow \phi(x,t) + \eta(x,t) \cdot \epsilon$
-
$\delta S = \int dt \int dx [\frac{m}{2} (\dot{\phi} + \epsilon \dot{\eta})^2 -\frac{\beta a^2}{2}(\partial_x \phi + \epsilon \partial_x \eta )^2 -\frac{m}{2} \dot{\phi}^2 + \frac{\beta a^2}{2} (\partial_x \phi)^2 ] $
-
忽略$\epsilon^2$以上高阶项,可以得到:
$ \int dx \int dt \epsilon (m \dot{\phi} \dot{\eta} - \beta a^2 \partial_x \phi \partial_x \eta) =0$
分步积分,并假定$\eta(x,t)$在无穷远处(积分的上下界处)为0,即得:
$m \partial^2_t \phi - \beta a^2 \partial^2_x \phi = 0$,场的拉氏运动方程(波动方程)。
-
波动方程的一般解:$\phi_{\pm}(x \mp vt) $,代入运动方程不难得到:
$m v^2 \partial^2_t \phi_{\pm} - \beta a^2 \partial^2_x \phi_{\pm} = 0$
即:$v = a \sqrt{\frac{\beta}{m}}$。
-
不失一般性,可以选取平面波作为正交归一的基底展开任意波函数。
-
-
经典场论的哈密顿形式
-
按照分析力学,引入正则动量 $\pi(x) = \frac{\partial \mathcal{L}(\phi, \partial_x \phi, \dot{\phi})}{\partial \dot{\phi}} = m \dot{\phi}$
-
泊松括号:{$\pi(x), \phi(x')$} $= -\delta(x-x')$
-
哈密顿密度:$\mathcal{H}(\pi, \partial_x \phi, \dot{\phi}) = \pi \dot{\phi} - \mathcal{L}(\phi,\partial_x \phi, \dot{\phi}) = \frac{\pi^2}{2m} + \frac{\beta a^2}{2} (\partial_x \phi)^2$
-
哈密顿量可以写成哈密顿密度的积分
$H[\pi, \phi] = \int dx \mathcal{H} = \int dx [\frac{\pi^2}{2m} + \frac{\beta a^2}{2} (\partial_x \phi)^2]$
-
-
场量子化
-
提升$\pi(x)$和$\phi(x)$为场算符$\hat{\pi}(x), \hat{\phi}(x)$,满足$[\hat{\pi}(x), \hat{\phi}(x')] = -i\hbar \delta(x-x')$。
-
傅里叶变换到动量空场算符$\pi_k, \phi_k$
$\pi_k = \frac{1}{\sqrt{L}} \int_0^{L} dx e^{ikx} \pi(x)$
$\phi_k = \frac{1}{\sqrt{L}} \int_0^{L} dx e^{-ikx} \phi(x)$
-
验证关系:$\pi_{-k}= \pi^{\dagger}_k$ (已知$\pi(x)^\dagger = \pi(x)$)。
-
量子哈密顿量可以写成简正模式的和
$H = \int dx \mathcal{H} = \int dx \frac{1}{2m L} (\sum_k e^{-ikx} \pi_k)^2 + \frac{\beta a^2}{2 L} (\sum_k ik e^{ikx} \phi_k)^2$
$=\sum_k (\frac{1}{2m} \pi_k \pi_{-k} + \frac{\beta a^2 k^2}{2} \phi_k \phi_{-k})$
$=\sum_k (\frac{1}{2m} \pi_k \pi_{-k} + \frac{m \omega_k^2}{2} \phi_k \phi_{-k})$
其中$\omega_k = v k$,$v = \sqrt{\frac{\beta a^2}{2m}}$为波速
如果将$\pi_{-k} \pi_k$ 视为$|\pi_k|^2$,$\phi_k \phi_{-k}$视为$|\phi_k|^2$,则量子哈密顿量非常类似于一个谐振子。
-
-
引入场的产生消灭算符
$a_k = \sqrt{\frac{m\omega_k}{2 \hbar}} (\phi_k +\frac{i}{m\omega_k} \pi_{-k})$
$a_k^\dagger = \sqrt{\frac{m\omega_k}{2 \hbar}} (\phi_{-k} - \frac{i}{m\omega_k} \pi_{k})$
作业:验证 $[a_k,a_k^\dagger] = 1$
$a_k^\dagger$ 表示产生一个$k$-模式玻色子的产生算符,$a_k$表示消灭算符,$n_k=a^\dagger_k a_k$表示$k$-模式的粒子数。
将哈密顿量写成对角形式
$H = \sum_k \hbar \omega_k (a_k^\dagger a_k + \frac{1}{2})$。
-
比较声子的两种导出方式(1)分立格点推导的优势在于直观、简单、具有启发性,但缺点在于推导过程不够一般;(2)先取连续极限,然后正则量子化的做法系统、规范、具有普适性。
Slides & Video
-
Video lectures (two, by Sandro Scandolo, ICTP), please click the icon below.
Discussions
- An online discussion (c.a. 90 min, via Wechat or Dingtalk) will be arranged.
Homework
-
长波极限下的运动方程:对于简单原子链,请证明在长波极限下运动方程可以化为连续介质波动方程
$\frac{d^2 u}{d t^2} = v^2 \frac{d^2 u}{d x^2}$,其中$v$为弹性波的波速。
-
考虑一个两周期原子链,耦合弹性系数按照$\beta_1$和$\beta_2$交替,写出原子链的运动方程,并求解本征运动模式和本征能量。
-
验证算符对易子:
(1)从 $[\pi(x), \phi(x')] = -i\hbar \delta(x-x')$,导出$[\pi_k, \phi_{k'}] = -i\hbar \delta_{k,k'}$;
(2)继续导出$[a_k, a^\dagger_{k'}] = \delta_{k,k'}$,玻色子对易关系。
[assigned: 30-March-2020, due: 06-April-2020]
