第二章晶体衍射

Crystal Diffraction


翠铜矿 dioptase

晶体从外观上能够识别吗？需要从微观层面考察晶体的微观结构！


紫水晶	金属铁	绿松石	玻璃制品

扫描隧道显微镜（STM, 1981）通过针尖的量子隧穿电流的大小可以直接“读取”电子密度、形貌特征等，使得人们第一次可以直接观察到原子的有序排列。但是，STM仅限于观察金属的表面，无法观察到体态（bulk）的微观结构。
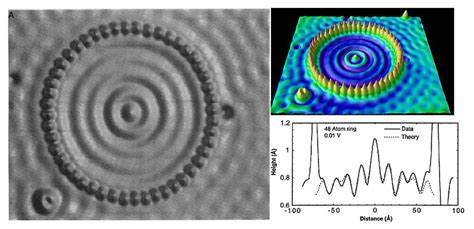
其他局域观测方法包括X-射线光电子能谱（XPS）等。
要观察体态的微观结构，需要采用衍射方法，包括电子显微镜，中子衍射，X-射线衍射等，这些方法采用电子/中子/光子的波动性，观察晶格的倒空间。
通过X射线衍射实验（劳厄，1912年，慕尼黑大学），人们第一次确认了晶体的周期结构。

衍射的亮斑对应倒空间的格矢，并进一步对应实空间的一族晶面。

1. 劳厄方程与倒易点阵 (Reciprocal lattice)

为引入倒格矢，考虑在布拉维格子上的X-射线衍射问题：入射波为$e^{i (\bf{k}\cdot\bf{r} - \omega t})$，在格点$\bf{r=R}$处发生反射，沿着$\bf{k'}$继续传播，波函数为$e^{i (\bf{k'}\cdot\bf{r} - \omega' t})$。
- 弹性散射，原子附近的电子云随入射波震荡，并发射相同波长/频率的反射波，$\omega' = \omega$，且$|\bf{k}|=|\bf{k'}|$。
- 波从$\bf r_0$出出发，经原子反射后反射到达$\bf r_f$处，波函数为：
  
  $ e^{i k \cdot (R-r_o) } \times e^{i \bf{k'} \cdot (r_f-R) } = e^{i(\bf{k'} \cdot r_f - k \cdot r_0)} \times e^{i (\bf{k'} - k) \cdot R }$
- 假设观察者足够远，看到$k'$方向的彼此平行的出射波，其强度需要对任意$R_I$求和，即$|\sum_I e^{i (\bf{k'} - k) \cdot R_I} |^2$。
- 对于满足劳厄方程$\bf e^{i (\bf{k'} - k) \cdot R } \equiv 1$条件的衍射情况，将在$\bf{k'}$方向看到相干衍射。
  
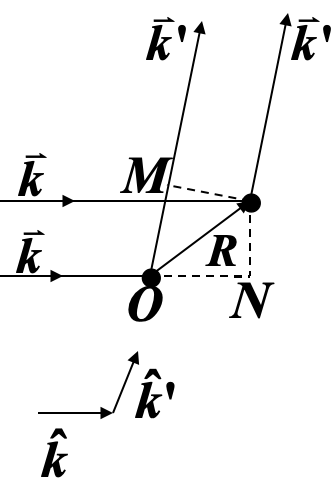
  因此，想要看到相干衍射峰，对衍射波的波矢变化$\bf \Delta k = k'-k$是有严格要求的。下面我们会看到，这个实际上是约定了一组特殊的矢量集，称为倒格矢集合{$G$}。
满足下面条件的矢量$G$ 被定义为倒格矢：对于布拉维格子的任意格矢$R_I$，都满$G \cdot R_I = 2 \pi n$，其中$n$为整数，使得$e^{i G \cdot R_I} = 1$。
- 倒格矢集合$G$构成布拉维格子，称为倒易点阵。倒易点阵必为布拉维格子（证明？）
- 若$G_1,G_2,G_3$满足$e^{i G_i \cdot R_I} = 1$，则$G_1,G_2,G_3$的任意组合也满足。因此，恰当选取一组初基矢量，就可以将所有满足$e^{i G \cdot R_I} = 1$的矢量$G$表达出来。
- 按照下面公式（验证是否满足倒格子初基矢量关系）从实空间中初基矢量构造出倒格子初基矢量：
  
  $ b_i = 2\pi \frac{a_j \times a_k}{\Omega} $
  
  其中$\Omega = a_i \cdot (a_j \times a_k)$，且$i,j,k=1,2,3$满足轮换关系，如当$i=1,j=2$时，$k=3$。
- 倒格子初基矢量（$b_j$）与正格子初基矢量（$a_i$）满足关系：
  
  $a_i \cdot b_j =2 \pi \delta_{ij}$
  
  例如，$a_1 \cdot b_1 = 2 \pi$，而$a_1 \cdot b_2 = a_1 \cdot b_3 = 0$。
- 利用倒格子初基矢量$b_j$可以将倒格矢展开$G_{h,k,l}= h b_1 + k b_2 + l b_3$，其中$h,k,l$为整数（也恰好是与倒格矢$G$相垂直晶面族的晶面指数，见下文介绍）。
倒易点阵举例
- 一维倒格子：一维布拉维格子只有一种，相应也只有一种倒格子。
  
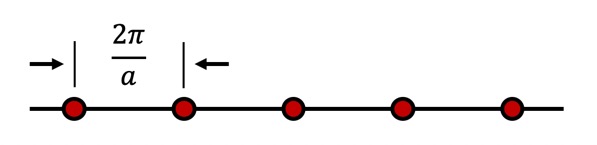
  倒格矢为$b_1=\frac{2\pi}{a}$，$a$为晶格常数。
- 二维倒格子
  
  可以引入虚拟的第三方向$a_3$（大小无关）垂直于$a_1,a_2$，不难看出可以按照$ b_i = 2\pi \frac{a_j \times a_k}{\Omega} $公式生成出在$a_1$-$a_2$平面内的倒格矢$b_1,b_2$（二维晶格忽略$b_3$分量）。
  
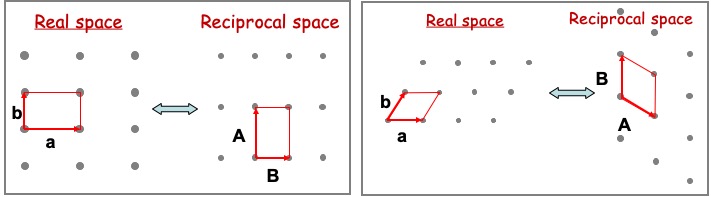
  长方（rectangular）格子的倒格子仍是长方格子，满足$A =\frac{2\pi}{|a|} \hat{a}_1$, $B =\frac{2\pi}{|b|} \hat{b}_2$
  
  单斜（oblique）格子的倒格子仍是单斜格子，满足$A \perp b$且$A\cdot a = 2\pi$，$B \perp a$且$B \cdot b = 2\pi$
  
  问题： 三角格子的倒格子是什么？（追问： 有心长方的倒格子是什么？）
- 三维倒格子
  - 简单立方为自身的倒格子
  - 面心立方和体心立方互为对方的倒格子
  - 问题： 底心正交格子的倒格子是什么？

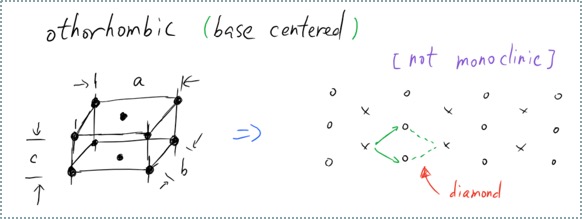
2. 晶面反射与布拉格定律

晶面族与倒格矢

定理： 考虑布拉维格子中任意一组晶面族，设晶面间距为$d$，必存在一组倒格矢与该晶面族垂直，其中最短的非零倒格矢长度为$\frac{2\pi}{d}$。

证明： 用构造法，构造一组矢量$G_h= h \frac{2\pi}{d} \hat{n}$（$h$为整数），然后证明其为倒格矢。

按照定义，因布拉维格子可以被完全解理为晶面族，取原点位于晶面族某个晶面A，则从原点到另一个晶面族成员B上的某个格点间距记为$R$，可以看到

$e^{iG \cdot R} = e^{ih \frac{2\pi}{d} \cdot m d}=e^{ihn}$，其中$m d$为AB两晶面之间的间距。

因此，我们证明$G_h= h \frac{2\pi}{d} \hat{n}$为倒格矢，而其中最短（非零）者长度为$\frac{2\pi}{d}$。
- 逆定理： 倒格子中存在一组倒格矢$G_h = h \frac{2 \pi}{d}$（$h$为整数，倒格矢最短者为$\frac{2\pi}{d}$），则在正格子中必存在一组晶面族与该组倒格矢正交，且最小晶面间距为$d$。
- 由逆定理得知，对于指数为$(h,k,l)$的晶面，间距为$\frac{2\pi}{|h b_1 + k b_2 + l b_3|}$，因此晶面指数越小（大），间距越大（小）。晶体的解理面往往都是小指数晶面，衍射实验观察到的也主要是小指数晶面。
  
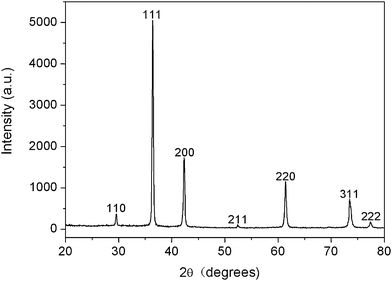
  NaCl的X-射线衍射峰
倒格子晶向指数与正格子晶面指数

倒格矢与晶面族存在一一对应关系，因此可以采用倒格矢$G=hb_1 + kb_2+lb_3$中的(h,k,l)来标记。
- 与操作定义等价：垂直倒格矢$G$的晶面族在$a_1,a_2,a_3$轴上的截距设为$x_i a_i$，其中$i=1,2,3$，代表A，B，C点（下图所示）。
  
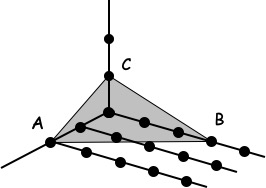
  考虑到A，B，C点在$G$方向的投影需相等，且$a_i \cdot b_j = 2 \pi \delta_{i,j}$。因此$x_1 h =x_2 k=x_3 l $，因此在三轴上的截距坐标分别正比于$x_1:x_2:x_3=1/h:1/k:1/l$。
晶面反射

在晶体衍射中，根据劳厄衍射方程，出射波与入射波的波矢相差倒格矢。通过倒格矢与晶面族的对应关系，可以籍此将晶体衍射看成X射线在晶面族上的镜面反射。

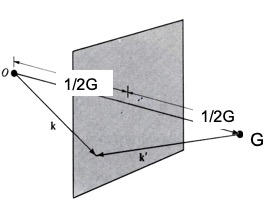
晶面反射布拉格定律

如图所示，入射波$k$与出射波$k'$相差倒格矢$G$，则几何上恰好等于在与$G$垂直的晶面上发生反射。
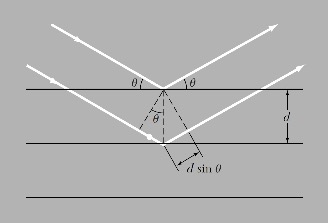
布拉格定律

假设两束波均以波矢$k$入射，掠入角为$\theta$（见上图），在两个相距$d$的晶面上发生反射，在$k’$方向上观测，发生相干增强衍射极大的条件为光程差为波长$\lambda$整数倍（即相差$2\pi$整数倍），即：

$2d \sin(\theta) = n \lambda$，$n=1,2,…$为整数。
- 劳厄方程是晶体衍射的倒空间表示，更为本质；布拉格定律是晶体衍射的实空间表述，十分直观。二者等价（请推导）。
- 布拉格定律直观地说明，发生衍射的条件需要波长$\lambda \leq 2d$，长波（如可见光，波长~500 nm）无法发生晶体衍射，X射线波长在0.1 nm以下，可以将晶格当做天然”光栅“，发生衍射。
- 整数$n$代表衍射级数，例如简单立方晶格(110)晶面，可以发生$n=1$的一级，也可以发生$n>1$的高级衍射，对应的原则上是同一晶面族(110)。注意(110)同时也标记着与该晶面族垂直的最短倒格矢h=1,k=1,l=0.
- 为了区分不同$n$的衍射极大，考虑到$n>1$所对应$\Delta k$为最小倒格矢的整数$n$倍，因此实践中常常采用这些垂直晶面族但非最小倒格矢的晶向指数，如(220), (330)等，来代表$n=2,3$级衍射。虽然这些指数作为晶面指数并没有约分，但有其意义。但是需要注意一点，即这些指数不是严格的晶面指数，不能从这些扩大的指数来计算晶面间距（要注意第二节中逆定理，晶面间距由最段倒格矢指数计算）。


NaCl的X-射线衍射峰


晶面反射	布拉格定律

3. 结构因子与消光

在上面介绍倒格子中，我们提及布拉维格子的倒格子必为布拉维格子，这使得倒格子较之正格子更为抽象和”干净“。通过晶格衍射我们可以间接观察到倒格子，并反推正格子。另一方面，我们知道，通过将正格子格点置换为物理实在的基元，我们得到晶体结构。在倒格子中是否也有对应的考虑？当考虑晶格结构的基元时，晶体衍射需要如何将这些具体的物理内容纳入到衍射谱分析中去呢？这一节我们就讨论在倒格子之外，具体基元对晶体衍射的重要修正。

具体的说，我们需要对晶体衍射的峰强度进行修正，附加两个因子：原子内部形状带来的因子$f$和复杂基元带来的几何结构因子$S$。

原子形状因子（atomic form factor, $f$）

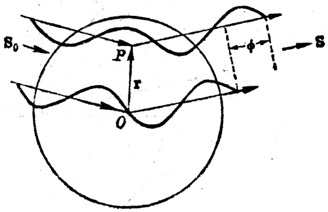
在考虑布拉维格子衍射时，我们将每个格点视为抽象的几何点处理。在实际晶格结构中，需要将基元内容放置在格点处，光受到电子云的散射，晶体衍射会受到具体原子形状因子的影响。衍射峰强度需要乘以原子形状因子$f_j(G) = \int n_j(r) e^{i(k'-k)r} dr = \int n_j(r) e^{iGr} dr$

其中$n_j(r)$为在第$j$个原子附近，空间$r$点处的电子密度n_j(r)$，因此原子形状因子随具体原子不同而不同，且允许呈现出各向异性的特征。

然而，在下面的讨论中，为简化计，我们认为原子均为球形，形状因子为与空间角度无关的常数$f_0$。
几何结构因子（geometric structure factor, $S$）与消光条件

在NaCl的衍射峰结构中，我们观察到，并不是所有立方晶系的衍射峰都出现了，这是因为米勒指数是按照简单立方的元胞和初基矢量来定义的，在这种定义下面心立方和体心立方都不再是布拉维格子，而是基元中包含多于1个点的”非布拉维格子”。下面我们来分析这种情况下所附加的几何结构因子计算。
- 结构因子计算可以视为基元的“形状因子”，区别在于此时原子的位置是分立的，形状因子的积分被$p$个原子的求和替代：
  
  $S(G) = \sum_{j=0}^{p-1} f_j(G) e^{i G \cdot d_j}$
  
  其中$d_j$为第$j$个原子的相对位置矢量（即相对布拉维格点的位置），$G$为倒格矢，$f_j(G)$为第$j$个原子的形状因子（为简化问题，以下均取为与$G$无关的常数$f_0$）。
- 体心立方的几何结构因子
  
  采用惯用晶胞，则基元中包含2个格点，位置分别为$d_0 = 0$和$d_1=\frac{a}{2} (\hat{x} + \hat{y} + \hat{z}$ （$\hat{x}, \hat{y}, \hat{z}$为三个方向的单位矢量）。
  
  对于倒格矢$G = \frac{2\pi}{a} (h \hat{x} + k \hat{y} + l \hat{z})$
  
  结构因子为：
  
  $S(G) = f_0 (e^{i G \cdot d_0} + e^{i G \cdot d_1}) = f_0 (1 + e^{i \pi (h+k+l)})$。
  
  因此，对于$h+k+l$为偶数情况，衍射峰按照劳厄/布拉格衍射正常出现；对于$h+k+l$为奇数的情况，$S(G) = 0$，不出现衍射峰，称为晶面消光。
- 面心立方的几何结构因子
  
  基元中包含4个格点，位置分别为$d_0=0$，$d_1=\frac{a}{2} (\hat{x} + \hat{y})$，$d_2=\frac{a}{2} (\hat{x} + \hat{z})$，以及$d_1=\frac{a}{2} (\hat{y} + \hat{z})$。因此，结构因子为：
  
  $S(G) = f_0 \sum_j e^{i G \cdot d_j} = f_0 (1 + e^{i \pi (h+k)} + e^{i \pi (h+l)} + e^{i \pi (k+l)})$。
  
  因此，对于晶面指数/倒格矢$h,k,l$全为奇数或全为偶数时，劳厄/布拉格衍射正常发生；而当部分为奇数部分为偶数时，发生消光。
- 出现消光的晶面是因为基元中不同位置的格点/原子所反射的出射波相位互相抵消，这是考虑基元物理内容后给结晶衍射带来的复杂性。
- 注意，不仅仅在体心立方和面心立方中，因人为约定，带来不平庸的几何结构因子。一般的情况下，因为基元中包含多于一个以上的原子时，都存在几何结构因子。
- 因此，对应于“晶体结构=布拉维点阵+基元”，我们可以类似写下：晶体衍射=倒格子+结构因子。注意，这里的"+“应该不能简单理解加法的加，而是复合结构（或者说“乘”也许更为恰当）。倒格子本身均为布拉维格子，而结构因子会在此基础上改变倒格子不同格点的强度，产生更为复杂的结构，在特殊情况下会将部分倒格点消去（如上面所讨论的面心立方和体心立方情况）。
- 在讨论晶体衍射时，布拉维格子的重要性凸显出来。例如，氯化铯结构我们如果错误地当成体心立方，就会得不到正确的晶体衍射分析。
X射线谱分析
- 二维晶格衍射分析：入射X射线（或电子波束），可以得到二维晶格的衍射图像，可以类似三维情况建立二维晶格衍射的理论。
- 衍射图像代表二维晶格的倒格子，每一个晶向对应一个衍射极大（倒格矢），晶向间距$d=\frac{2\pi}{|G|}$，$G$为垂直这些互相平行原子链的最短倒格矢。
  
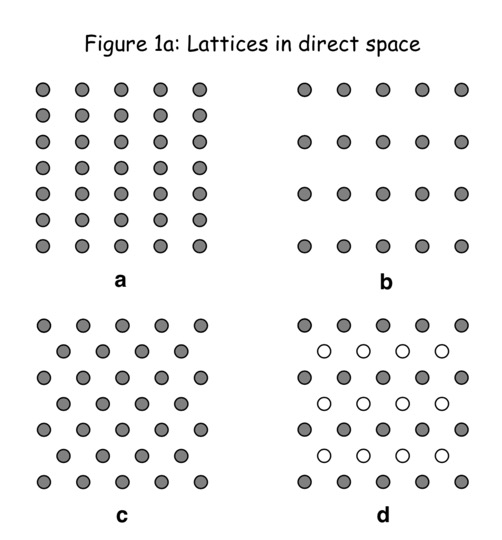
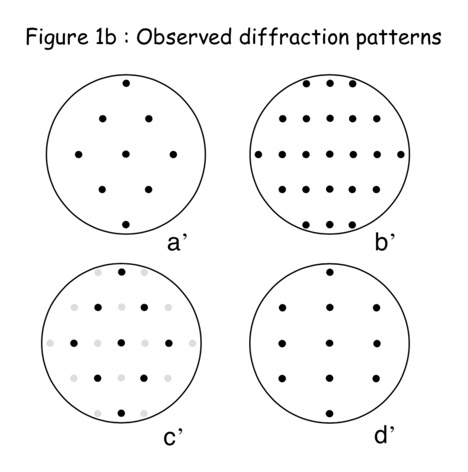
  晶面反射衍射斑点
  
  请问如何实空间和衍射结果如何对应起来？
- 三维晶格衍射分析：在某次实验中得到如下衍射图谱，已知此三维晶格属于立方晶系，即简单立方、面心立方或体心立方的一种。根据此衍射结果是否能够唯一确定晶体的为微观结构？
  
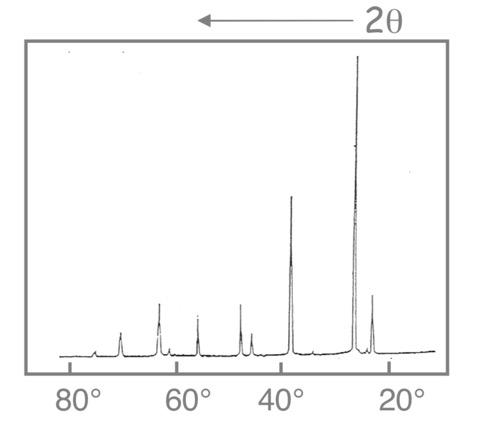
  实验测得晶体衍射结果，采用单色光进行衍射，前两个衍射峰的角度为23.6$^\circ$6与27.1$^\circ$。
  - 首先按照布拉格定律，并代入晶面指数与晶面间距关系进行分析。
  根据布拉格定律 $2d\sin{(\theta)}=n \lambda$，可以导出
  
  $\sin{(\theta)} = \lambda \frac{n}{2d} = \lambda \frac{n|G|}{4\pi}$
  
  $ = \frac{\lambda}{4\pi} \sqrt{(\frac{2\pi}{a})^2 (h^2+l^2+k^2)} = \frac{\lambda}{2a} \sqrt{h^2+l^2+k^2}$，其中$h,k,l$为布拉格衍射极大对应的倒格矢晶向指数。
  - 按照前面分析的消光条件，不难得到下面的列表
    
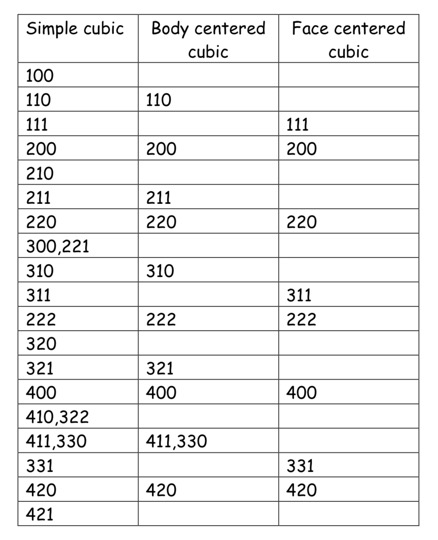
    三种立方晶系成员的衍射峰对应倒格矢
  - 提示：按照头两个峰的角度比值确定晶面指数$(h,k,l)$。


晶面反射	衍射斑点


实验测得晶体衍射结果，采用单色光进行衍射，前两个衍射峰的角度为23.6$^\circ$6与27.1$^\circ$。


三种立方晶系成员的衍射峰对应倒格矢

4. 实验方法

按照劳厄方程，能够在固定角度的单晶样品上产生单色光衍射的波矢角度方向十分有限，为了观察到衍射斑点，需要采用一定的实验方法。

劳厄法：采用连续波长的X射线观察晶体衍射

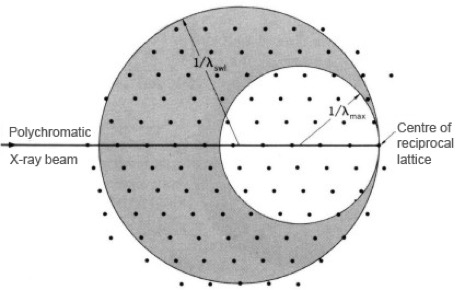
劳厄（多色光）法，图示为埃瓦尔德球
转晶法：单色光入射，转动晶体观察衍射极大
粉末法：单色光在粉末多晶上，相当于同时转动多个晶体样本，同时看到多个晶面，效率高

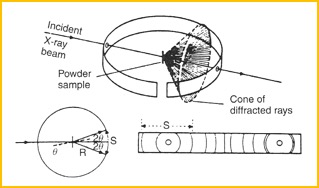
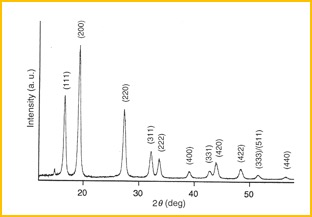
德拜（粉末）法粉魔法观察的衍射图谱
AuCu₃合金的晶体衍射：Au和Cu的合金形成简单立方结构，并存在两种相，有序相与无序相。在有序相中，Au占据中心位置（0,0,0），而3个Cu原子占据(1/2,1/2,0)，(1/2,0,1/2)和(0,1/2,1/2)三个位置。在无序相中，Au和Cu随机的占据上述4个位置。

(a)和(b)何者为有序相，何者为无序相？


劳厄（多色光）法，图示为埃瓦尔德球


德拜（粉末）法	粉魔法观察的衍射图谱


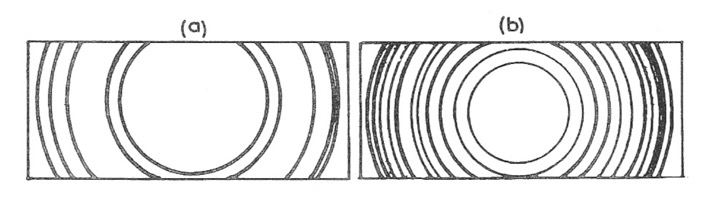
(a)和(b)何者为有序相，何者为无序相？

问题： 请写下两种相的结构因子，并判断图中衍射条纹分别属于哪种相。假设Au和Cu的原子形状因子分别是$f_{Au}$和$f_{Cu}$。

Slides & Video

Slides for Chapter 2 can be downloaded
Video lectures (two, by Sandro Scandolo, ICTP), please click the icon below.
- Lecture 05
- Lecture 06

Discussions

An online discussion (c.a. 30 + 30 min, via Wechat or Dingtalk) will be arranged.

Homework

1. 请证明倒格子原胞体积$\Omega$^*与正格子（布拉维格子）原胞体积$\Omega$的乘积为$(2\pi)$³。
2. 证明劳厄方程/布拉格定律的等价表述：入射波波矢$\bf{k}$与倒格矢$\bf{G}$满足关系$\bf{k} \cdot \frac{1}{2} G= (\frac{1}{2}G)^2$，则产生布拉格衍射。并籍此说明该表述的一个直观图像：入射波矢出发点位于原点$O$时，当终点位于布里渊区边界上时，发生布拉格衍射。
  
  [assigned: 06-March-2020, due: 13-March-2020]
3. 证明晶面族与倒格矢关系的逆定理，即给定倒格矢，必存在与之正交的晶面族。
4. 请从劳厄衍射方程推导出布拉格定律。
5. 请画出三角格子的倒格子，并找出倒格子的魏格纳-赛兹（WS）原胞。原格子的晶格常数为$a$，请计算这个WS原胞（一个正多边形）的边长，以及中心到任意一条边的高，然后计算WS原胞的面积。
  
  [assigned: 10-March-2020, due: 17-March-2020]
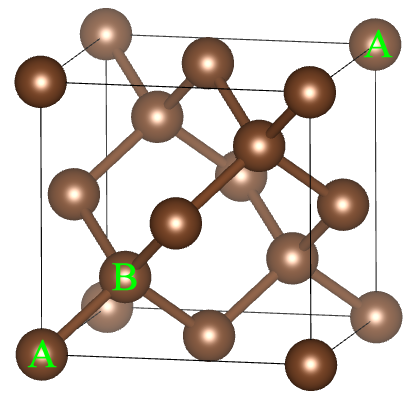
6. 请计算金刚石的结构因子，假设碳原子的形状因子为常数$f_0$。
7. 根据课堂讨论的三维立方晶系衍射图谱分析，根据衍射角度，按照X射线波长$\lambda=1.54\overset{\circ}{\rm{A}}$，确定具体晶体结构，并定出晶格常数$a$。
8. 请写下AuCu₃合金两种相的结构因子，并列表写下两种情况的头3个衍射峰对应的射倒格矢晶向指数。
  
  [assigned: 13-March-2020, due: 20-March-2020]

Last updated on Feb 22, 2020

Edit this page

第二章 晶体衍射