第五章 晶格热力学
Crystal Thermodynamics
 |
|---|
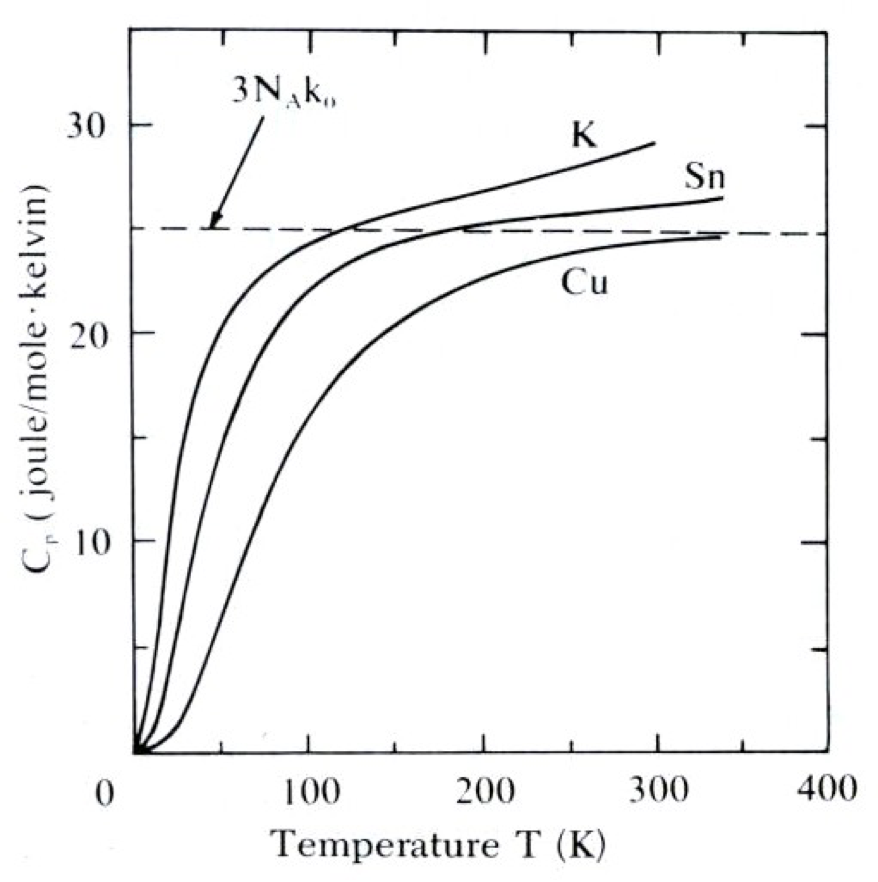
| 晶格比热,在高温呈现普适的德隆-佩蒂特定律,在低温反常的衰减到零。 |
- 通过对格波量子化,我们将晶格振动转化为无相互作用声子气的玻色-爱因斯坦统计,通过这一量子统计方法,我们得以破解晶格反常低温比热的谜题。
0. 自由声子气体的玻色-爱因斯坦统计
-
高温经典极限: 德隆—佩蒂特定律
-
在高温极限下,晶体满足能均分定理:$3N$个原子共计$3N$个动能项和$3N$个势能项,每项有平均能量$\frac{1}{2} k_B T$,$k_B$为玻尔兹曼常数,而$T$为温度。
-
不难得出,晶体在高温下平均能量为$u=3Nk_BT$,比热为$C = 3Nk_B$,这是一个普适的常数,无论晶体由何种成分组成,晶格结构如何,高温极限热容量都满足此关系,称为德隆—佩蒂特定律 (Dulong-Petit‘s law)。
-
-
量子声子气体: 将$q$-模式谐振子处于第$n$激发态视为激发$n$个声子,每个声子携带$\hbar \omega_q$的能量量子。在上一章内容中,我们也曾经介绍过,通过长波极限下场的正则量子化,晶格振动的声子激发可以类比“光场”中激发的能量量子—光子,体现了波动性与粒子性的统一。
-
按照玻色-爱因斯坦分布,温度为$T$化学势为0的玻色巨正则系综,能量为$\hbar \omega$的声子占据数$n = \frac{1}{e^{\hbar \omega/k_B T}-1}$。
-
平均能量与热容量
为了统计方便,我们在能量空间做统计,若能量$\omega$处的声子态密度(简并度)为$g(\omega)$,代表在能量$\omega$附近$d\omega$范围内存在$g(\omega) d\omega$的模式数,因此总声子数目为:
$\frac{1}{e^{\hbar \omega_q/k_B T}-1} g(\omega) d\omega$
注意: $g(\omega)$不是声子密度,是声子态密度,或者说振动模式密度,代表在能量$\omega$附近$d\omega$范围内有多少激发能量近简并的振动模式。
考虑到每个声子携带一份能量量子$\hbar \omega$,则声子气总能量可以如下计算:
$u = \int_0^{\omega_m} \frac{\hbar \omega}{e^{\hbar \omega/k_B T}-1} g(\omega) d\omega $
比热容计算:
$C_v = (\frac{\partial u}{\partial T})_V=\int_0^{\omega_m} k_B (\frac{\hbar \omega}{k_B T})^2 \frac{e^{\hbar \omega/k_B T}}{(e^{\hbar \omega/k_B T}-1)^2} g(\omega) d\omega$
其中积分上限$\omega_m$是有限值,需要保证总自由度守恒,即:
$\int_0^{\omega_m} g(\omega) = 3N$.
1. 固体热容量与爱因斯坦模型
 |
|---|
| 阿尔伯特 爱因斯坦 (1879-1955) |
-
爱因斯坦模型的提出(1907年):假设固体中原子的热运动可以视为$3N$个量子谐振子的振动,各自独立的激发声子,晶体比热可以通过声子气的玻色—爱因斯坦统计计算出来。
-
爱因斯坦模型可以正确给出晶体比热的高温行为,并得到比热低温衰减到零的现象,揭示出理解固体物理现象需要使用能量量子这一重要的论断。固体低温比热行为与光电效应一起,称为量子论的早期重要支柱。
-
爱因斯坦模型声子热容量:
-
爱因斯坦模型的所有$3N$个振动模式以固定的频率$\omega_E$振动(爱因斯坦原始提议是$N$原子振动所对应的$3N$个谐振子,虽然这并不确切)对应的态密度为$g(\omega) = 3N \delta(\omega - \omega_E)$。
-
计算出晶格能量
$u = 3N \frac{\hbar \omega_E}{e^{\hbar \omega_E/k_B T}-1}$
-
对应热容量
$C_V = 3N k_B (\frac{\hbar \omega_E}{k_B T})^2 \frac{e^{\hbar \omega_E/k_B T}}{(e^{\hbar \omega_E/k_B T}-1)^2}$
可以更紧凑的写成
$C_V= 3N k_B (\frac{\theta_E}{T})^2 \frac{e^{\frac{\Theta_E}{T}}}{(e^{\frac{\Theta_E}{T}}-1)^2}$,
其中$\hbar \omega_E = k_B \theta_E$,$\theta_E$也称为爱因斯坦温度,代表原子谐振子的特征温度(能量)。
-
高温极限:$C_V \to 3 N k_B$,普适常数,德隆—佩蒂特定律。
低温极限:$C_V \to e^{-\Theta_E/T}$,指数衰减。
[作业:推导爱因斯坦模型热容量的高温和低温极限]
-
-
爱因斯坦认真每个原子是不相互作用的独立谐振子,这一假设并不正确(否则晶体将不能传递声波),所以爱因斯坦模型虽然正确的得到了在低温衰减到零的比热容$C$,但确得到了$C$在低温指数衰减这样与实验定量上并不相符合结论。
2. 声子态密度
-
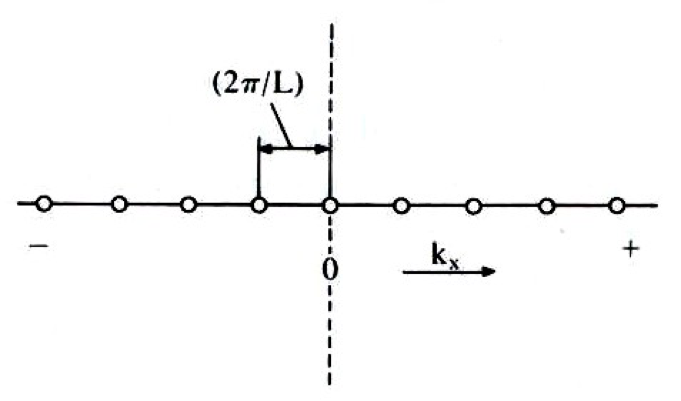
一维原子链声子态密度,$q$空间中,间距$dq$所包含的简正模式数目为$dn=\frac{L}{2\pi} dq$。
-
能量空间中,间距$d\omega$内包含的简正模式数为 $dn = g(\omega) d\omega$,其中$g(\omega)$称为态密度函数。已知色散关系,则可以求得态密度。
-
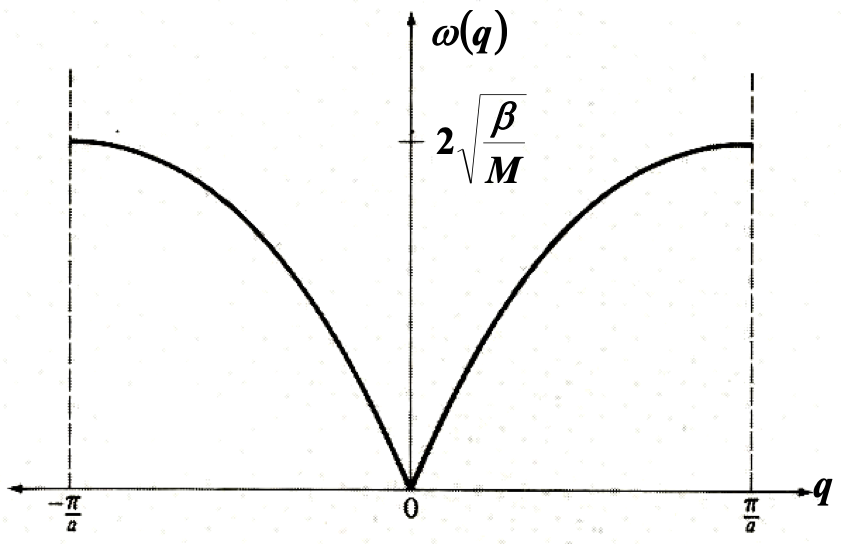
一维原子链的色散关系为$\omega = 2 \sqrt{\frac{\beta}{M}} |\sin{\frac{qa}{2}}|$
-
态密度为:$g(\omega) = dn/d\omega = \frac{L}{2\pi} (2 \cdot dq)/d\omega = \frac{L}{\pi} \frac{1}{\omega'}$。
-
$\omega' = 2 \sqrt{\frac{\beta}{M}} \cdot \frac{a}{2} \cos{\frac{qa}{2}} = \frac{a}{2} \omega_m \cos{\frac{qa}{2}}$,其中$ \omega_m =\sqrt{\frac{4\beta}{M}}$为最大激发能量(位于$q=\pm \frac{pi}{a}$处)。
-
因此,$g(\omega) = \frac{L}{\pi} \frac{2}{a \omega_m} \frac{1}{\cos{\frac{qa}{2}}} = \frac{2N}{\pi \omega_m \sqrt{(1 - \sin^2{\frac{qa}{2}})}} = \frac{2N}{\pi \sqrt{(\omega_m^2 - \omega^2)}} $。
- $\omega \to 0$极限下,$g(\omega) \to \frac{2N}{\pi \omega_m}$,态密度为常数。
- $\omega \to \omega_m$,$g(\omega) \to \infty$,态密度为发散。
- $\omega > \omega_m$,态密度为零。
-
双原子链存在光学支$\omega_+$和声学支$\omega_-$,总态密度是两支之和$g(\omega) = g_+(\omega^+) + g_-(\omega^-)$。
-
-
三维晶格振动存在一支纵波与两支横波,因此对于N个原子组成的三维晶体,简正模式总数为$3N$。暂时先忽略这一因素,按照其中一支来简单计算。
-
按照$\omega(q)$关系,可以知道声子激发的等能面形成球面,半径变化$dq$范围内包含的简正模式数$dn$ 可以如下计算:
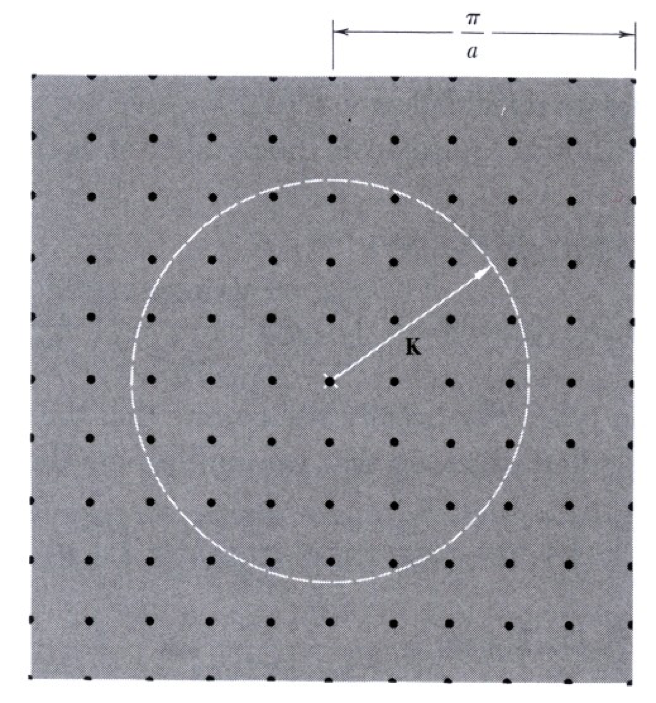
$dn = \frac{L^3}{(2\pi)^3} 4\pi q^2 dq = \frac{V}{2\pi^2} q^2 dq$
-
按照态密度定义$dn = g(\omega) d\omega$,可以计算出
$g(\omega) = \frac{V}{2\pi^2} q^2 \frac{1}{d\omega/dq}$
-
-
一般等能面的态密度计算公式
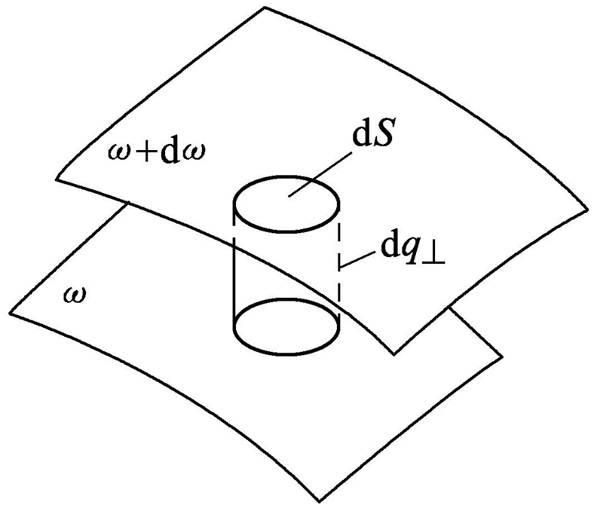
- $q$空间计算: $dn = \frac{V}{(2\pi)^3} \int dS \cdot dq_{\perp}$
- $\omega$空间:$dn = g(\omega) d\omega$,其中按照定义$d\omega =\nabla_q \omega \cdot dq_{\perp} $,即波矢变化乘以能量梯度。
- 态密度一般表达式:$g(\omega) = \frac{V}{(2\pi)^3} \int dS \cdot \frac{1}{\nabla_q \omega}$
- 因此,有具体的色散关系表达式$\omega(q)$,人们就可以计算出对于求解热力学量的重要信息—态密度$g(\omega)$。
- 态总数守恒:$\int g(\omega) d\omega = 3N$,$N$为格点数目,“3"代表1支纵波2支横波。
3. 德拜模型
-
德拜模型取长波极限下的线性色散,即$\omega = v q$,其中 $v$为格波波速,而$q$代表波矢的模。德拜模型中需要引入一个截止频率$\omega_m$,在此之下,能量-动量色散关系为线性,等能面为球面。不难看出,这是对实际晶体格波的一个理想假设。
-
计算德拜模型态密度:$g(\omega)= 3 \frac{V}{2\pi^2} \frac{\omega^2}{v^2} \frac{1}{v} = \frac{3V \omega^2}{2\pi^2 v^3}$,其中因子"3"考虑了三支弹性波的贡献。
-
德拜模型比热计算:
平均能量:$u = \int_0^{\omega_m} \frac{\hbar \omega}{e^{\hbar \omega/k_B T}-1} \frac{3V \omega^2}{2\pi^2 v^3} d\omega$
比热容:$C_V = (\frac{\partial u}{\partial T})_V= \frac{3V}{2\pi^2 v^3} \int_0^{\omega_m} k_B (\frac{\hbar \omega}{k_B T})^2 \frac{e^{\hbar \omega/k_B T} \omega^2}{(e^{\hbar \omega/k_B T}-1)^2} d\omega$
-
德拜截止频率与德拜温度:
$\int_0^{\omega_m} g(\omega) d\omega = \int_0^{\omega_m} \frac{3V \omega^2}{2\pi^2 v^3} d\omega = 3N$
得出德拜截止频率为 $\omega_m = (\frac{6 \pi^2 N}{V})^{1/3} v$,并引入德拜温度$\theta_D = \frac{\hbar \omega_m}{k_B}$,代表德拜模型的温度尺度。
-
可以按照$T\gg \theta_D$ 和 $T\ll \theta_D$ 来讨论德拜模型的高温与低温极限:
首先引入变量 $x = \frac{\hbar \omega}{k_B T}$ 和 $x_m = \frac{\hbar \omega_m}{k_B T} = \frac{\theta_D}{T}$ 来简化比热表达式:
$C_V = \frac{3V}{2\pi^2 v^3} \int_0^{\omega_m} k_B (\frac{\hbar \omega}{k_B T})^2 \frac{e^{\hbar \omega/k_B T} \omega^2}{(e^{\hbar \omega/k_B T}-1)^2} d\omega $
$ \quad = \frac{3V}{2\pi^2 v^3} \int_0^{x_m} k_B x^2 \frac{e^x \omega^2}{(e^x-1)^2} d\omega $
$ \quad = \frac{3V k_B}{2\pi^2 v^3} (\frac{k_BT}{\hbar})^{3} \int_0^{x_m} \frac{e^x x^4}{(e^x-1)^2} dx$
$ \quad = 3 k_B \frac{V}{2\pi^2} (\frac{k_BT}{\hbar v})^{3} \int_0^{x_m} \frac{e^x x^4}{(e^x-1)^2} dx$
-
高温极限($T\gg\theta_D$):
$x$为小量,$e^x \simeq 1 + x$,积分得到
$C_V = 3 k_B \frac{V}{2 \pi^2} (\frac{k_BT}{\hbar v})^{3} \frac{1}{3} x_m^3$
其中 $x_m^3 =(\frac{\theta_D}{T})^3 = (\frac{\hbar \omega_m}{k_B T})^3 = (\frac{\hbar v}{k_B T})^3 \frac{6 \pi^2 N}{V} $
得到 $C_V = 3 N k_B$,即回到德隆-佩蒂特定律。
-
低温极限($T\ll \theta_D$):
注意到$(\frac{T}{\theta_D})^3 = (\frac{k_B T}{\hbar v})^3 \frac{V}{6 \pi^2 N}$,可以进一步将比热简写为
$C_V = 9 N k_B (\frac{T}{\theta_D})^3 \int_0^{x_m} \frac{e^x x^4}{(e^x-1)^2} dx$
在低温极限下,$x_m = \frac{\theta_D}{T} \to \infty$,利用
$\int_0^{\infty} \frac{e^x x^4}{(e^x-1)^2} dx = \frac{4}{15} \pi^4$ 为常数
可以得到著名的德拜$T^3$律
$C_V = \frac{12 \pi^4}{5} N k_B (\frac{T}{\theta_D})^3$
-
-
德拜-爱因斯坦(Debye-Einstein)唯象模型
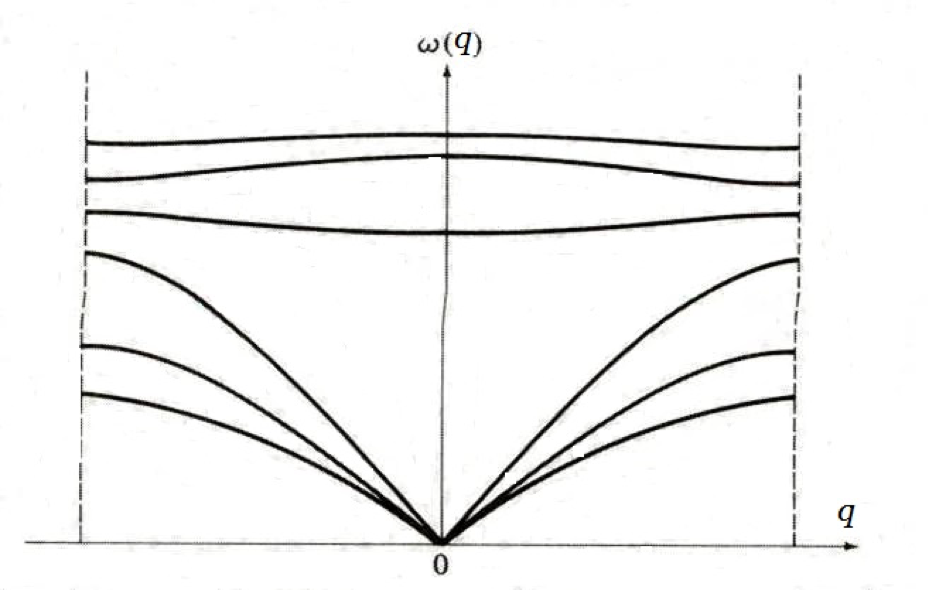
实际晶体振动中既存在光学支也存在声学支,需要采用德拜-爱因斯坦混合模型来描述。 - 德拜模型对于声学支描述较好,适用于处理低温的热力学性质;爱因斯坦模型对于光学支是很好的近似,处理中间-高温的热力学性质时不可忽略。
- $g(\omega) = g_E(\omega) + g_D(\omega)$,态密度是二者的混合,可以唯象地描述固体的比热。
-
实际晶体的声子谱
-
第一性原理计算提供了对声子谱的计算。
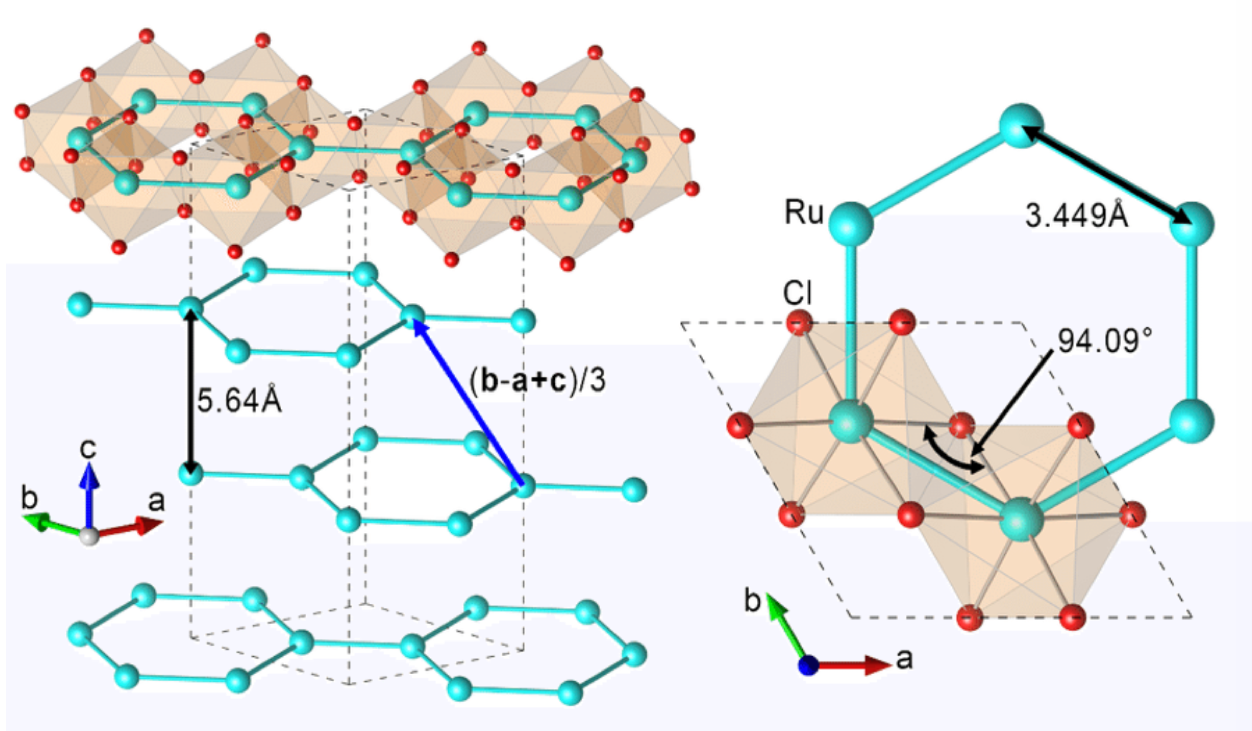
二维磁性材料$\alpha$-RuCl$_3$的晶体结构(原胞中包含几个原子?) 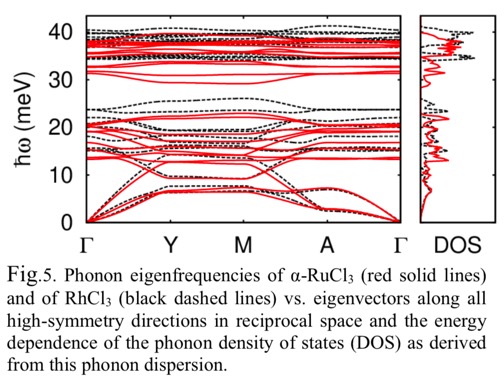
声子谱第一性原理计算结果。 -
中子散射,非弹性X射线散射等,也可以从实验上得到晶体的声子谱。
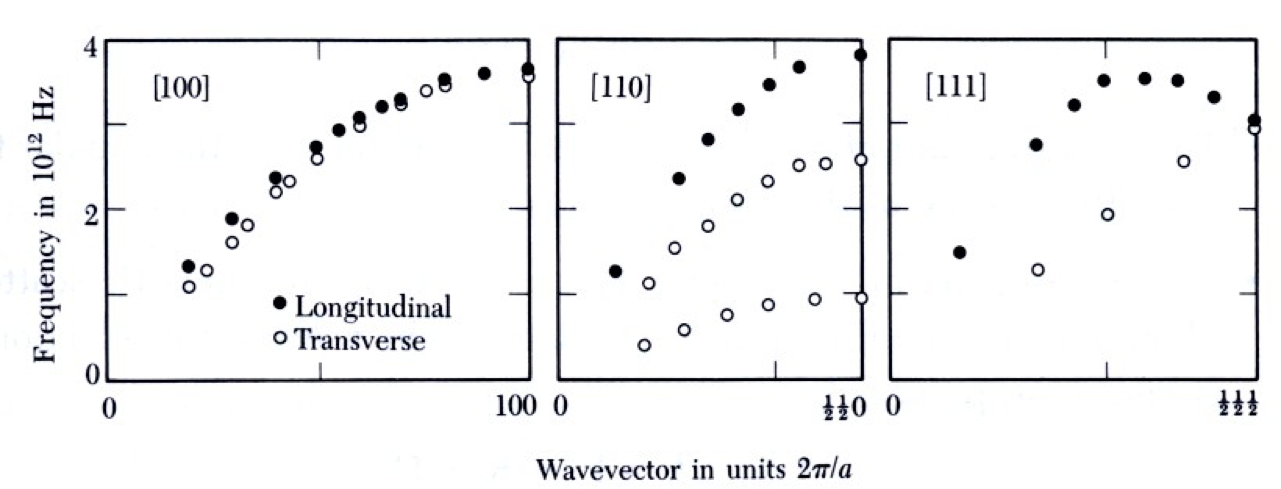
90K下,金属Na单晶沿不同方向的声子谱。
-
4. 非谐效应
-
理想晶体中原子所受势场为平方势,对应激发的格波为自由玻色场,即自由声子气。声子之间彼此不发生相互作用。
-
矛盾: 声子之间无法传递能量,无耗散亦不能建立热平衡,也无法理解固体的晶格热输运。甚至不能解释热胀冷缩现象。
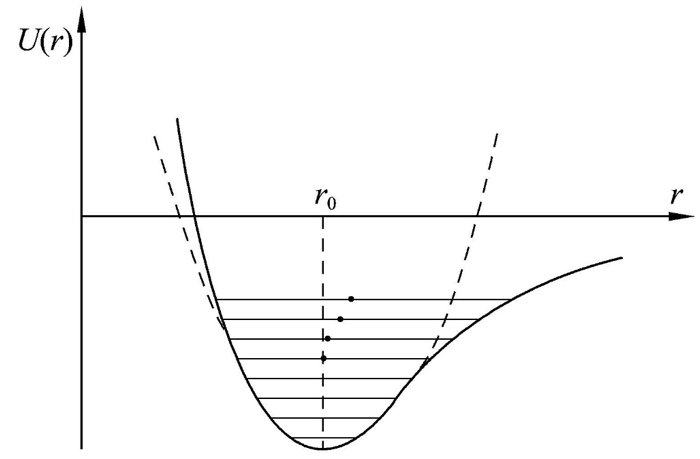
原子势场:热运动导致原子在势阱内运动。 -
非谐效应:考虑到实际固体中原子会偏离谐振子势,玻色场不再自由,需要考虑声子之间的相互作用。
-
非谐效应导致两大物理现象:热胀冷缩和热输运。
-
“热胀冷缩“
核心是计算热膨胀系数 $\alpha = \frac{1}{V} (\frac{\partial V}{\partial T})_P$ (等压),为此,我们做若干准备工作:
-
热身活动: 定容热容恒等式
-
晶格自由能:$F=U-TS$
全微分形式:$dU = TdS - PdV$
-
熵的全微分:$dS = (\frac{\partial S}{\partial T})_V dT + (\frac{\partial S}{\partial V})_T dV$
-
结合二者得到:$dU = T (\frac{\partial S}{\partial T})_V dT + [(\frac{\partial S}{\partial V})_T - P] dV$
-
对比:$dU = (\frac{\partial U}{\partial T})_V dT + (\frac{\partial U}{\partial V})_T dV$
-
得到定容热容恒等式:$C_V = (\frac{\partial U}{\partial T})_V = T (\frac{\partial S}{\partial T})_V$
-
-
物态方程
-
不妨从自由玻色子系统出发($\beta = \frac{1}{k_B T}$):
$\mathcal{F}=-\frac{1}{\beta} \ln{\lgroup \Pi_q \frac{e^{-\frac{1}{2} \hbar \omega_q \beta}}{1-e^{-\beta \bar \omega_q}} \rgroup }$
$ \quad = \sum_q \frac{1}{2} \hbar \omega_q + \sum_q \frac{1}{\beta} \ln{(1-e^{-\beta \hbar \omega_q})}$
-
按照定义 $P = (\frac{\partial F}{\partial V})_T$(回忆 $\mathcal{Z} = \sum e^{-\beta (E+ PV)}$),可以得到:
$P = \frac{\partial}{\partial V} (\sum_q \frac{1}{2} \hbar \omega_q) + \sum_q \frac{\partial (\hbar \omega_q)}{\partial V} \frac{e^{-\beta \hbar \omega_q}}{1-e^{-\beta \hbar \omega_q}}$
$\quad =\frac{\partial}{\partial V} (\sum_q \frac{1}{2} \hbar \omega_q) + \sum_q \frac{\partial(\hbar \omega_q)}{\partial V} \langle n_q \rangle$
$\quad =\sum_q \frac{\partial(\hbar \omega_q)}{\partial V} (\frac{1}{2} + \langle n_q \rangle )$
$\quad =\sum_q \frac{\partial \ln{(\hbar \omega_q)}}{\partial \ln{V}} \frac{\hbar \omega_q}{V}(\frac{1}{2} + \langle n_q \rangle )$
$\quad =\sum_q \frac{\partial \ln{(\hbar \omega_q)}}{\partial \ln{V}} \frac{u_q}{V}$
$\quad =\sum_q \gamma_q \frac{u_q}{V}$
其中 $\langle n \rangle_\beta = \frac{1}{e^{\beta \hbar \omega}-1}$ 为玻色子占据数,
而$u_q =( \frac{1}{2} + \langle n_q \rangle) \hbar \omega_q$ 为$q$-模式平均能量,
$\gamma = \frac{\partial \ln{(\hbar \omega)}}{\partial \ln{V}}$ 称为格林艾森参数。
-
理想固体物态方程
以上为自由声子气带来的固体压强,结合固体结合能$U_0$随体积变化带来的贡献$-\frac{dU}{dV}$,我们得到理想固体物态方程:
$P = -\frac{dU}{dV} + \gamma \frac{u}{V}$
其中$u = \sum_q u_q$,$\gamma$为平均格林艾森参数。
-
-
热膨胀系数
回忆:$\alpha = \frac{1}{V} (\frac{\partial V}{\partial T})_P$
按照$P$的全微分:$dP = (\frac{\partial P}{\partial T})_V dT + (\frac{\partial P}{\partial V})_T dV$
得到 $(\frac{\partial V}{\partial T})_P = -(\frac{\partial P}{\partial T})_V/(\frac{\partial P}{\partial V})_T$
-
体弹性模量 $B = -V (\frac{\partial P}{\partial V})_T$
-
膨胀系数 $\alpha = \frac{1}{B} (\frac{\partial P}{\partial T})_V = \frac{1}{B} \sum_q \gamma_q \frac{\partial}{\partial T}(\frac{u_q}{V})$
-
用平均格林艾森参数 $\gamma$ 取代 $\gamma_q$,则不难得到:
-
理想固体无热膨胀:
振动频率 $\omega_q$ 与体积无关(为什么?),格林艾森参数$\gamma_q = 0$,因此膨胀系数 $\alpha = 0$。
-
格林艾森定律:
膨胀系数 $\alpha = \frac{\gamma}{B} \sum_q c_q = \frac{\gamma}{B} c_V$,$c_V$为定容比热。
-
高温极限:$c_V \to 3Nk_B$,$\alpha \to const.$,普适常数。
-
低温极限:$c_V \to T^3$,$\alpha \propto T^3$(有趣!)
-
-
-
晶格热输运**
Slides & Video
-
Video lectures (two, by Sandro Scandolo, ICTP), please click the icon below.
Tutorial
-
德拜—爱因斯坦模型计算离子晶体的热容
考虑一维离子晶体,晶格常数为$2a$,$N$个晶胞总长为$L=2Na$。为计算热容,色散关系做如下近似:
- 声学支:用德拜模型,$\omega = v q$,定义$\omega_m$为最大截止频率,对于1D情况,它处于布里渊区的边界。
- 光学支:用爱因斯坦模型,$\omega = \omega_E$,声子激发为无色散局域模。
问题:
-
利用波恩—冯卡曼边界条件,有多少振动模处于$\omega$到$\omega+d\omega$范围内。
-
考虑光学支,计算一个振子的平均能量,并计算相应的热容,讨论其高温($T\to \infty$)和低温($T\to 0$)极限。
-
计算一个声学振子(振动模式)的平均能量和相应的热容,讨论高温和低温极限。
-
给出总能量和热容,并讨论低温和高温极限,
-
计算数值:按照$a=0.28$nm,$\nu_E=9.5\times 10^12$Hz,声速$v = 8800m\cdot s^{-1}$,请计算爱因斯坦温度$\theta_E$和德拜温度$\theta_D$。
-
画出声学-光学支比热和总热容的示意图,并计算温度为20 K时,声学支和光学支对热容的贡献分别是多少。
Hints:$\int_0^{\infty} \frac{x}{e^x-1} dx = \frac{\pi^2}{6}$,普朗克常数$h=6.63\times10^{-34} J \cdot s$,$k_B=1.38\times 10^{-23} J/K$。
Homework
-
推导爱因斯坦模型的高温和低温极限。
-
推导二维晶格振动的德拜模型比热,并讨论其高温与低温极限。
-
讨论如何构造爱因斯坦-德拜模型的具体计算拟合实验曲线过程。
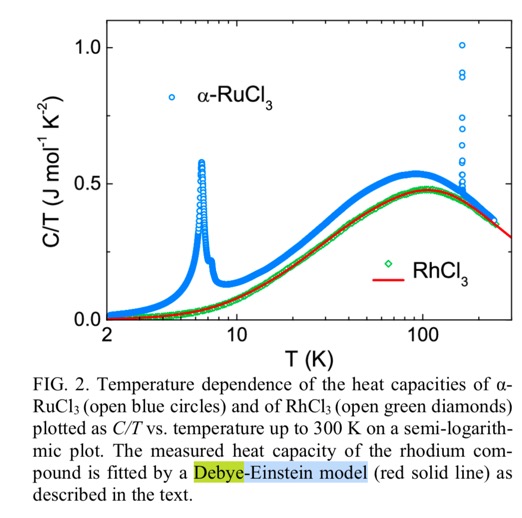
RhCl$_3$的比热主要为声子贡献,以这个例子为参考,提出方案,建立德拜-爱因斯坦唯象理论拟合其比热曲线。
[assigned: 07-April-2020, due: 14-April-2020]
-
证明在简谐近似下,晶体的声子定容比热和定压比热无差别,并导出单位体积两种比热的关系 $c_p - c_v = B T \alpha^2$。
[assigned: 14-April-2020, due: 21-April-2020]
